Question

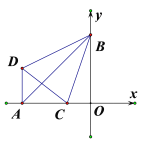
【题目】如图,在平面直角坐标系中，A(-3,0),B(0,3),DA⊥x轴，点C在OA上且∠CDB=∠ OBD，则∠CBD的度数是（ ）

A.72°B.60°C.45°D.36°

Answer 1

【答案】C

【解析】

延长DC交y轴于点E，连接AE，先证明△ADE≌△CEB，再通过角度转换得到∠DBA=∠CBE，即可求出∠CBD的度数.

延长DC交y轴于点E，连接AE，

∵A(-3，0)，B(0，3)，

∴OA=OB，

∵∠CDB=∠ OBD，

∴ED=EB，

∵DA⊥x轴，

∴DA∥BE，

∴∠ADC=∠CEB，

∴△ADE≌△CEB，

∴∠AED=∠CBE，

∴∠DBA=∠CBE，

∵∠ABO=45°，

∴∠OBC+∠CAB=45°，

∴∠DBA+∠ABC=45°，

∴∠CBD=45°，

故选C.