题目内容
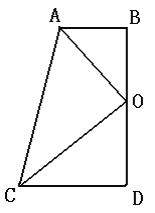
【题目】如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC.
(1)求证:CO平分∠ACD;
(2)求证:OA⊥OC;
(3)求证:AB+CD=AC.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
试题(1)过点O作OE⊥AC于E,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;
(2)利用“HL”证明△ABO和△AEO全等,根据全等三角形对应角相等可得∠AOB=∠AOE,同理求出∠COD=∠COE,然后求出∠AOC=90°,再根据垂直的定义即可证明;
(3)根据全等三角形对应边相等可得AB=AE,CD=CE,然后证明即可.
试题解析:
(1)过点O作OE⊥AC于E,
∵∠ABD=90゜,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OC平分∠ACD;
(2)在Rt△ABO和Rt△AEO中,
![]() ,
,
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOE+∠COE=![]() ×180°=90°,
×180°=90°,
∴OA⊥OC;
(3)∵Rt△ABO≌Rt△AEO,
∴AB=AE,
同理可得CD=CE,
∵AC=AE+CE,
∴AB+CD=AC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目