题目内容
【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF、CG.
(1)求证:EF∥CG;
(2)求点C、点A在旋转过程中形成的![]() 、
、![]() 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
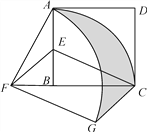
【答案】(1)证明见解析;(2) S阴影=![]() .
.
【解析】试题分析:(1)根据正方形的性质可得AB=BC=AD=2,∠ABC=90°,再根据旋转变化只改变图形的位置不改变图形的形状可得△ABF和△CBE全等,根据全等三角形对应角相等可得∠FAB=∠ECB,∠ABF=∠CBE=90°,全等三角形对应边相等可得AF=EC,然后求出∠AFB+∠FAB=90°,再求出∠CFG=∠FAB=∠ECB,根据内错角相等,两直线平行可得EC∥FG,再根据一组对边平行且相等的四边形是平行四边形判断出四边形EFGC是平行四边形,然后根据平行四边形的对边平行证明;
(2)求出FE、BE的长,再利用勾股定理列式求出AF的长,根据平行四边形的性质可得△FEC和△CGF全等,从而得到S△FEC=S△CGF,再根据S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG列式计算即可得解.
试题解析:(1)证明:在正方形ABCD中,AB=BC=AD=2,∠ABC=90°.∵△BEC绕点B逆时针旋转90°得到△ABF,∴△ABF≌△CBE,∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE,∴∠AFB+∠FAB=90°.∵线段AF绕点F顺时针旋转90°得线段FG,∴∠AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC∥FG.∵AF=CE,AF=FG,∴EC=FG,∴四边形EFGC是平行四边形,∴EF∥CG;
(2)解:∵AD=2,E是AB的中点,∴BF=BE=![]() AB=
AB=![]() ×2=1,∴AF=
×2=1,∴AF=![]() =
=![]() =
=![]() ,由平行四边形的性质,△FEC≌△CGF,∴S△FEC=S△CGF,∴S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG=
,由平行四边形的性质,△FEC≌△CGF,∴S△FEC=S△CGF,∴S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG=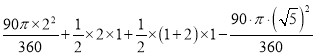
=![]() .
.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案