题目内容
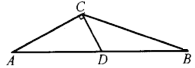
【题目】已知△ABC中,AB =1,D是AB的中点,∠ACD = 90°,∠DCB = 45°,求BC的长.
【答案】![]()
【解析】
延长CD,过B点作BE⊥CD的延长线于E点,利用倍长中线定理得到△ACD≌△BED,再利用∠DCB = 45°得到△BCE为等腰直角三角形,设CD=x,则DE=x,BE=2x,利用Rt△BDE求出x2的值,再根据勾股定理求出BC2,即可得到BC的长.
如图,延长CD,过B点作BE⊥CD的延长线于E点,
∵∠ACD = 90°,D是AB的中点
∴∠BED=∠ACD = 90°,AD=BD,
又∠ADC=∠BDE
∴△ACD≌△BED,
∴CD=DE
∵∠DCB = 45°,
∴△BCE为等腰直角三角形,CE=BE
设CD=x,则DE=x,BE=2x,
在Rt△BDE中BD2=DE2+BE2
即![]() 2=x2+(2x)2
2=x2+(2x)2
解得x2=![]() ,∴(2x)2=
,∴(2x)2=![]()
∴BC2=CE2+BE2=![]()
∴BC=![]() .
.


练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目