题目内容
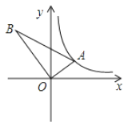
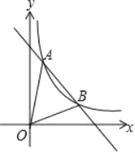
【题目】如图，已知反比例函数y=kx-1（k＞0）的图象与一次函数图象y=﹣x+4交于a、b两点，点a的纵坐标为3．
（1）求反比例函数的解析；
（2）y轴上是否存在一点P，使2∠APB=∠AOB？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】（1）
；（2）P（0，
）或（0，-）
【解析】
（1）根据A在y=-x+4上，且点A的纵坐标为3，于是得到A（3，1），由于点A在反比例函数
的图象上，即可得到结论；（2）根据勾股定理得到OA=
，根据2∠APB=∠AOB，于是推出点P在以O为圆心，以OA为半径的圆上，得到OP=，即可得到结论．
解：（1）∵A在y=-x+4上，且点A的纵坐标为3，得到A（3，1），
∵点A在反比例函数的图象上，得k=3，
∴反比例函数的解析为：．
（2）如图所示，
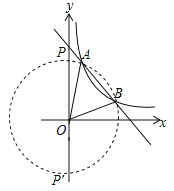
∵A（3，1），∴OA=，
∵2∠APB=∠AOB，
∴点P在以O为圆心，以OA为半径的圆上，
∴OP=，
∵点P在y轴上，
∴P（0，）或P（0，
）．
鸿图图书寒假作业假期作业吉林大学出版社系列答案
【题目】某公司为了到高校招聘大学生，为此设置了三项测试：笔试、面试、实习．学生的最终成绩由笔试面试、实习依次按3：2：5的比例确定．公司初选了若干名大学生参加笔试，面试，并对他们的两项成绩分别进行了整理和分析．下面给出了部分信息：
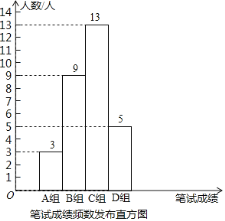
①公司将笔试成绩（百分制）分成了四组，分别为A组：60≤x＜70，B组：70≤x＜80，C组：80≤x＜90，D组：90≤x＜100；并绘制了如下的笔试成绩频数分布直方图．其中，C组的分数由低到高依次为：80，81，82，83，83，84，84，85，86，88，88，88，89．
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表：
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息，回答下列问题：
（1）这批大学生中笔试成绩不低于88分的人数所占百分比为 ．
（2）m＝ 分，若甲同学参加了本次招聘，他的笔试、面试成绩都是83分，那么该同学成绩排名靠前的是 成绩，理由是 ．
（3）乙同学也参加了本次招聘，笔试成绩虽不是最高分，但也不错，分数在D组；面试成绩为88分，实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分；若该公司最终录用的最低分数线为86分，请通过计算说明，该同学最终能否被录用？
