题目内容
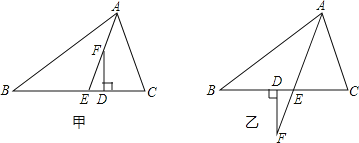
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
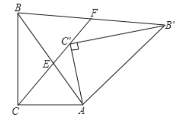
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
【答案】(1)见详解;(2)成立,证明见详解.
【解析】
(1) 根据三角形内角和定理以及角平分线的定义得到∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)=90°﹣
(180°﹣∠B﹣∠C)=90°﹣![]() (∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;
(∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;
(2)根据(1)可以得到∠AEC=90°+![]() (∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
解:(1)∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)
(180°﹣∠B﹣∠C)
=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵∠FEC=∠B+∠BAE,
则∠FEC=∠B+90°﹣![]() (∠B+∠C)
(∠B+∠C)
=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∵FD⊥EC,
∴∠EFD=90°﹣∠FEC,
则∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)成立.
证明:同(1)可证:∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠DEF=∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B).
(∠C﹣∠B).

 阅读快车系列答案
阅读快车系列答案【题目】问题背景:
学校广播站要招聘一名播音员,需考查应聘学生的应变能力、知识面、朗读水平三个项目,决赛中,小文和小明两位同学的各项成绩如下表,评委计算三项测试的平均成绩,发现小明与小文的相同.
测试项目 | 测试成绩 | |
小文 | 小明 | |
应变能力 | 70 | 80 |
知识面 | 80 | 72 |
朗诵水平 | 87 | 85 |
(1)评委按应变能力占10%,知识面占40%,朗诵水平占50%计算加权平均数,作为最后评定的总成绩,成绩高者将被录用,小文和小明谁将被录用?
(2)若(1)中应变能力占![]() ,知识面占
,知识面占![]() ,其中
,其中![]() ,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的
,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的![]() 的值.
的值.