题目内容
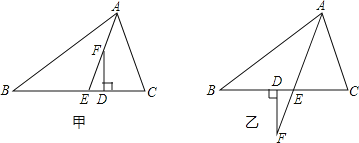
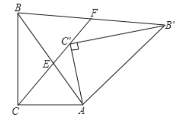
【题目】如图,![]() 是由
是由![]() 绕点
绕点![]() 顺时针旋转得到的,连结
顺时针旋转得到的,连结![]() 交斜边于点
交斜边于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() ;
;
(2)证明:![]() ;
;
(3)设![]() ,试探索
,试探索![]() 满足什么关系时,
满足什么关系时,![]() 与
与![]() 是全等三角形,并说明理由.
是全等三角形,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,见解析
,见解析
【解析】
(1)根据旋转的性质可以证得:△ACC′∽△ABB′,即可求解;
(2)根据旋转的性质可以证得:AC=AC′,AB=AB′,∠CAB=∠C′AB′,再根据∠AEC=∠FEB即可证明两个三角形相似;
(3)当β=2α时,△ACE≌△FBE.易证∠ABC=∠BCE,再根据CE=BE,即可证得.
(1)解:∵AC=AC′,AB=AB′,
∴![]()
由旋转可知:∠CAB=∠C′AB′,
∴∠CAB+∠EAC′=∠C′AB′+∠EAC′,即∠CAC′=∠BAB′,
又∵∠ACB=∠AC′B′=90°,
∴△ACC′∽△ABB′,
∵AC=3,AB=4,
∴![]() ;
;
(2)证明:∵Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,
∴AC=AC′,AB=AB′,∠CAB=∠C′AB′,
∴∠CAC′=∠BAB′,
∴∠ABB′=∠AB′B=∠ACC′=∠AC′C,
∴∠ACC′=∠ABB′,
又∵∠AEC=∠FEB,
∴△ACE∽△FBE.
(3)解:当β=2α时,△ACE≌△FBE.理由:
在△ACC′中,
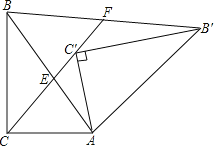
∵AC=AC′,
∴∠ACC′=∠AC′C=![]() =90°-α,
=90°-α,
在Rt△ABC中,
∠ACC′+∠BCE=90°,
即90°-α+∠BCE=90°,
∴∠BCE=90°-90°+α=α,
∵∠ABC=α,
∴∠ABC=∠BCE,
∴CE=BE,
由(2)知:△ACE∽△FBE,
∴△ACE≌△FBE.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目