题目内容
【题目】如图,点C、D在线段AB上,△PCD是等边三角形,且CD2=ADBC.
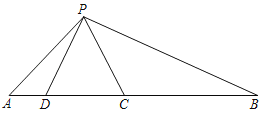
(1)求证:△APD∽△PBC;
(2)求∠APB的度数.
【答案】(1)见解析;(2)120°
【解析】
(1)CD2=ADBC可得AD:PC=PD:BC,又由△PCD是等边三角形,所以可求出∠ADP=∠BCP=120°,进而证明△ACP∽△PDB;
(2)由△APD∽△PBC,可得∠APD=∠B,则可求得∠APB的大小.
(1)证明:∵△PCD是等边三角形,
∴PD=PC=DC,∠PDC=∠PCD=60°,
∴∠ADP=∠BCP=120°,
∵CD2=ADBC,
∴AD:PC=PD:BC,
∴△APD∽△PBC;
(2)∵△APD∽△PBC,
∴∠APD=∠B,
∵∠B+∠BPC=60°,
∴∠APD+∠BPC=60°,
∴∠APB=60°+∠DPC=120°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目