题目内容
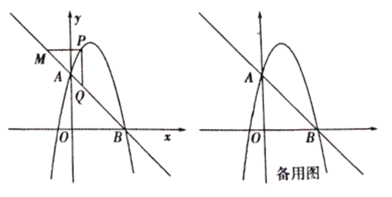
【题目】如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上任意一点(点
上任意一点(点![]() 与点
与点![]() 、
、![]() 不重合),以
不重合),以![]() 为一直角边在
为一直角边在![]() 的外部作
的外部作![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
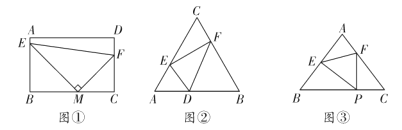
(1)在图![]() 中,若
中,若![]() ,
,![]() ,现将图
,现将图![]() 中的
中的![]() 绕着点
绕着点![]() 顺时针旋转锐角
顺时针旋转锐角![]() ,得到图
,得到图![]() ,那么线段
,那么线段![]() ,
,![]() 之间有怎样的关系,写出结论,并说明理由;
之间有怎样的关系,写出结论,并说明理由;
(2)在图![]() 中,若
中,若![]() ,
,![]() ,
,![]() ,
,![]() ,现将图
,现将图![]() 中的
中的![]() 绕着点
绕着点![]() 顺时针旋转锐角
顺时针旋转锐角![]() ,得到图
,得到图![]() ,连接
,连接![]() 、
、![]() .
.
①求证:![]() ;
;
②计算:![]() 的值.
的值.
【答案】(1)BE=CD,BE⊥CD;理由见解析;(2)①证明见解析;②170.
【解析】
(1)结论:BE=CD,BE⊥CD;只要证明△ABE≌△ACD,即可解决问题;
(2)①根据两边成比例夹角相等即可证明△BAE∽△CAD;
②由①得到∠BEA=∠CDA,再根据等量代换得到∠EGD=90°,即DG⊥BE,根据勾股定理计算即可.
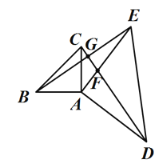
(1)BE=CD,BE⊥CD
理由:如图,设CD与BE、AE分别交于点G、F.
∵∠BAC=∠DAE=90°,∴∠BAC+∠CAE=∠DAE+∠CAE
即∠BAE=∠CAD
又∵AB=AC,AE=AD
∴△ABE≌△ACD(SAS)∴BE=CD,∠ADC=∠AEB
∵∠EAD=90°,∴∠ADC+∠AFD=90°,
又∵∠ADC=∠AEB,∠AFD=∠EFG
∴∠AEB+∠EFG=90°,
∴∠EGF=90°
∴BE⊥CD
(2)①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD
∵AB=5,AC=3,AE=10,AD=6
∴![]() ,
,![]() ,∴
,∴![]()
∴△BAE∽△CAD
②如图,延长DC交BE于点G
∵△BAE∽△CAD
∴∠BEA=∠CDA
在Rt△ADE中,∠ADE+∠AED=90°
∴∠CDA+∠CDE+∠AED=90°
∴∠BEA+∠AED+∠CDE=90°
∴∠EGD=90°
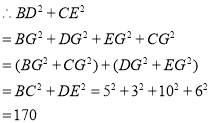

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目