��Ŀ����
����Ŀ���ۺ���ʵ������ֽ�е���ѧ
���ⱳ��
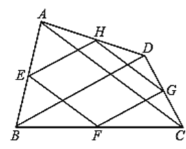
����ѧ����ϣ���ʦ���Ƚ�ƽ���ı���ֽƬABCD����ͼ����ʾ��ʽ�۵���ʹ��C���A�غϣ���D�䵽D�䴦���ۺ�ΪEF����ʱͬѧ�Ǻܿ�֤�ã���AEF�ǵ��������Σ���������ѧϰС��Ҳ���ֲ���������������������������⣮
��������
(1) �����ȡ�С�齫����ֽƬABCD��������ʽ�۵�����ͼ�ڣ������ص����֡�AEFǡ���ǵȱ������Σ������ABCD�ij�����֮���Ƕ��٣�
ʵ��̽��
(2)����־��С�齫����ֽƬABCD��EF�۵�����ͼ�ۣ�ʹB������AD���ϵ�B�䴦����B��G�۵���ʹD������D�䴦����B��D���F�㣮��̽���ı���EFGB����ʲô�����ı��Σ�
(3)��̽������ͼ��������BB�䣬���жϲ�֤����BB��G����״��

���𰸡���1������ABCD�ij�����֮��Ϊ![]() ����2���ı���EFGB����ƽ���ı��Σ����������������3����BB��GΪֱ�������Σ��������������
����2���ı���EFGB����ƽ���ı��Σ����������������3����BB��GΪֱ�������Σ��������������
��������
��1������![]() �ij�����֮��Ӧ��
�ij�����֮��Ӧ��![]() ����
����![]() �����ݵȱ������ε����ʿɵó�
�����ݵȱ������ε����ʿɵó�![]() �����ݾ��ε����ʿɵó�
�����ݾ��ε����ʿɵó�![]() ��
��![]() ���ٸ�������ǵ����Ǻ���ֵ���ɵó�
���ٸ�������ǵ����Ǻ���ֵ���ɵó�![]() ��
��![]() ����ϱ����֮��Ĺ�ϵ���ɵó�
����ϱ����֮��Ĺ�ϵ���ɵó�![]() ��
��
��2���ı���![]() ��ƽ���ı��Σ����ݾ��ε����ʿɵó�
��ƽ���ı��Σ����ݾ��ε����ʿɵó�![]() ���Ӷ��ó���ȵ��ڴ�����
���Ӷ��ó���ȵ��ڴ�����![]() ��
��![]() ��
��![]() �������ɷ��۵����ʿɵó�
�������ɷ��۵����ʿɵó�![]() ��
��![]() ���ɴ˼��ɵó�
���ɴ˼��ɵó�![]() ���Ӷ��ҳ�
���Ӷ��ҳ�![]() ��������Ա���ƽ�м���֤���ı���
��������Ա���ƽ�м���֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��3����![]() Ϊֱ�������Σ�����
Ϊֱ�������Σ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ������ƽ���ߵ����ʿɵó�
������ƽ���ߵ����ʿɵó�![]() ���ɷ��۵����ʿɵó�
���ɷ��۵����ʿɵó�![]() ���Ӷ��ɵó�
���Ӷ��ɵó�![]() �����ɵ��������ε����ʿɵó�
�����ɵ��������ε����ʿɵó�![]() ������ƽ���ߵ����ʼ��ɵó�
������ƽ���ߵ����ʼ��ɵó�![]() ���ɴ˼���֤����
���ɴ˼���֤����![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
�⣺��1������![]() �ij�����֮��Ӧ��
�ij�����֮��Ӧ��![]() ��
��
֤������![]() ��
��
![]() �ȱ������Σ�
�ȱ������Σ�
![]() ��
��
![]() �ı���
�ı���![]() Ϊ���Σ�
����
![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]()
![]() ��
��
��2���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
֤����![]() �ı���
�ı���![]() Ϊ���Σ�
����
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
�ɷ��۵����Կ�֪��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��
![]() �ı���
�ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��3����![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
֤��������![]() ��
��![]() �ڵ�
�ڵ�![]() ����ͼ��ʾ��
����ͼ��ʾ��
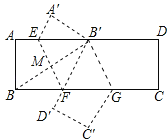
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ����������
����������
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�

 ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�