题目内容
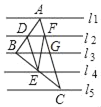
【题目】如图，l1∥l2∥l3∥l4∥l5，且l1，l2，l3，l4，l5中相邻两条直线之间的距离相等，△ABC的顶点A，B，C分别在l1，l3，l5上，AB交l2于点D，BC交l4于点E，AC交l2于点F，若△DEF的面积是1，则△ABC的面积是（ ）
A.3. 5B.4C.4.5D.5
【答案】B
【解析】
观察图形可以发现, 以BG为底,把△ABC 分成
与
计算较好,根据平行线分线段成比例定理,可得,的高与△DEF都相等,那么再求出底
与
的比例,按照三角形面积计算公式计算即可.
解：如图，
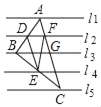
∵每相邻两条直线之间的距离为1，△DEF的面积为2，
∴
×DF×2＝1，
∴DF＝1，
∵DF∥BG，
∴
＝
＝，
∴BG＝2，
∴S△ABC＝S△ABG+S△BCG＝×2×2+ ×2×2＝4，
故选：B．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
