题目内容
【题目】阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线
经过B、C两点，顶点D在正方形内部．
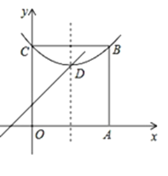
（1）直接写出点D（m，n）所有的特征线 ;
（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；
（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于y轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？
【答案】（1）y=n，x=m，y=-x+m+n，y=x-m+n；（2）
；（3）
或
【解析】
（1）根据特征线的定义以及性质直接求出点D的特征线；
（2）由点D的一条特征线和正方形的性质求出点D的坐标，从而求出抛物线解析式；
（3）分平行于x轴和y轴两种情况，由折叠的性质计算即可．
（1）∵点D
∴D的特征线是
（2）∵点D有一条特征线是
∴
∴
∵抛物线的解析式为
∴
∵四边形OABC是正方形，且D点为正方形的对称轴，
∴
∴
∴
将代入中
解得
∴抛物线的解析式为
（3）①如图，当点
在平行于y轴的D点的特征线时
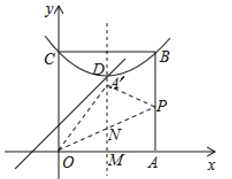
根据题意可得
∴
∴
∴
∴
∴抛物线需要向下平移的距离
②如图，当点在平行于x轴的D点的特征线时，设
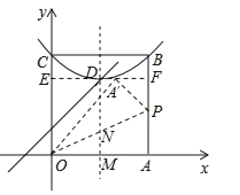
则
∴
设
在
中，
解得
∴
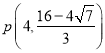
∴直线OP解析式为
∴
∴抛物线需要向下平移的距离
即抛物线向下平移或距离，其顶点落在OP上．
练习册系列答案
相关题目
