题目内容
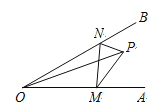
【题目】在正方形ABCD中,E对角线AC上一点,连接DE.
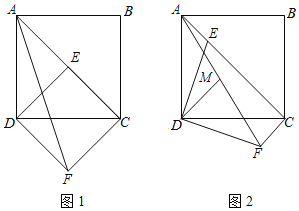
(1)如图1,若E为对角线AC中点,过点C、D分别作AC、DE的垂线相交于点F,连接AF,若AF=10,求正方形ABCD的面积;
(2)如图2,把△ADE绕点D顺时针旋转90°得到△CDF,连接AF,取AF的中点为M,连接DM,求证:4DM2+AE2=2DF2.
【答案】)(1)40;(2)详见解析
【解析】
(1)求正方形ABCD的面积,只需要先求出边长,可设a,再将直角三角形ACF的两条直角边用a来表示,再用勾股定理即可列出关于a的方程,解出并计算面积即可;
(2)要求证![]() ,即证
,即证![]() ,由旋转不变性知:
,由旋转不变性知:![]() ,故只需证
,故只需证![]() ,由直角三角形
,由直角三角形![]() 知右式等于
知右式等于![]() ,故只需证明
,故只需证明![]() ,而我们易得直角三角形
,而我们易得直角三角形![]() ,在这个三角形中
,在这个三角形中![]() ,而由旋转不变性知
,而由旋转不变性知![]() ,故只需求证
,故只需求证![]() ,过
,过![]() 点做
点做![]() 的平行线,构造平行线型全等,即可得到
的平行线,构造平行线型全等,即可得到![]() ,故只需求证:
,故只需求证:![]() ,通过全等即可.
,通过全等即可.
解:设正方形的边长为a,则对角线![]() ,
,
又![]() 若E为对角线AC中点,
若E为对角线AC中点,
∴![]() ,
,![]()
又∵![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∴![]()
∵在![]() 中,
中,![]() ,
,![]() span>,
span>,![]() ,
,![]() ,
,
∴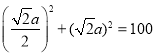 ,解得
,解得![]() ,
,
即正方形![]() 的面积为40.
的面积为40.
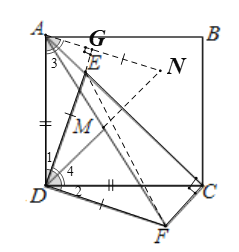
(2)过![]() 点做
点做![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ;
;
∵![]() ,
,
∴![]() ∽
∽![]() ,
,![]()
∴![]() ,
,
又∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,![]()
∴![]() ;
;
∵正方形![]() ,
,
∴![]() ;
;
∵△ADE绕点D顺时针旋转90°得到△CDF,
∴![]() ≌
≌![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ;
;
∵在![]() 和
和![]() 中
中
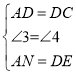
∴![]() ≌
≌ ![]() (SAS);
(SAS);
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
又∵![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]()
∴![]() ,即
,即![]() .
.

练习册系列答案
相关题目