题目内容
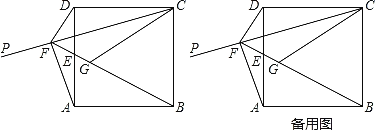
【题目】如图,Rt△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,点E在边AB上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P是线段AD上一动点,当半径为5的⊙P与△ABC的一边相切时,AP的长为_____.
【答案】![]() 或
或![]()
【解析】
设BD=x,由折叠性质得AD与CD,在Rt△ACD中由勾股定理列出x的方程,进而求得DE,得出⊙P不能与AB相切,进而分两种情况:⊙P与AC相切和⊙P与BC相切,过P作切线的垂线段,再根据相似三角形的比例线段便可求得结果.
解:设BD=x,由折叠知AD=BD=x,CD=16﹣x,
在Rt△ACD中,由勾股定理得,x2=82+(16﹣x)2,
解得,x=10,
∴CD=10,
∵AB=![]() =
=![]() =
=![]() ,
,
∴AE=BE=![]() AB=
AB=![]() ,
,
∴DE=![]() ,
,
∴点P是线段AD上运动时,⊙P不可能与AB相切,
分两种情况:①当⊙P与AC相切时,过点P作PF⊥AC于点F,如图1,
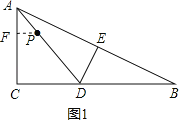
∴PF=5,PF∥CD,
∴△APF∽△ADC,
∴![]() ,即
,即![]() ,
,
∴![]() ;
;
②⊙P与BC相切时,过点P作PG⊥BC于点G,如图2,
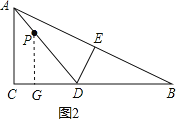
∴PG=5,PG∥AC,
∴△DPG∽△DAC,
∴![]() ,即
,即![]() ,
,
∴DP=![]() ,
,
∴AP=10﹣![]() =
=![]() ,
,
综上,AP的长为![]() 或
或![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】2020年3月“停课不停学”期间,某校采用简单随机抽样的方式调查本校学生参加第一天线上学习的时长,将收集到的数据制成不完整的频数分布表和扇形图,如下所示:
组别 | 学习时长(分钟) | 频数(人) |
第1组 | x≤40 | 3 |
第2组 | 40<x≤60 | 6 |
第3组 | 60<x≤80 | m |
第4组 | 80<x≤100 | 18 |
第5组 | 100<x≤120 | 14 |

(1)求m,n的值;
(2)学校有学生2400人,学校决定安排老师给““线上学习时长”在x≤60分钟范围内的学生打电话了解情况,请你根据样本估计学校学生“线上学习时长”在x≤60分钟范围内的学生人数.