Question

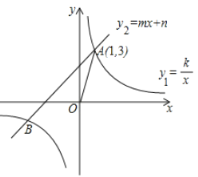
【题目】如图，反比例函数和一次函数相交于点，．

（1）求一次函数和反比例函数解析式；

（2）连接OA，试问在x轴上是否存在点P，使得为以OA为腰的等腰三角形，若存在，直接写出满足题意的点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1），；（2）(2，0) 或(，0)或(-，0)．

【解析】

（1）根据图象上点的坐标特征，以及待定系数法，即可得到答案；

（2）设P(t，0)，根据两点间的距离公式，分别表示出OA，AP，OP的长，结合OA=AP或OA=OP，列出方程，即可得到答案．

（1）∵反比例函数和一次函数相交于点，，

∴k=1×3=3，

∴，

∴-3a=3，解得：a=-1，

∴B(-3，-1)，

∴，解得：，

∴；

（2）设P(t，0)，

∵，

∴AP=，OP=，OA=，

∵为以OA为腰的等腰三角形，

∴OA=AP或OA=OP，

当OA=AP时，，解得：（不符合题意，舍去），

∴P(2，0)；

当OA=OP时，=，解得：t=±，

∴P(，0)或P(-，0)，

综上所述：存在点P，使为以OA为腰的等腰三角形，点P坐标为：(2，0) 或(，0)或(-，0)．