题目内容
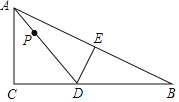
【题目】如图,已知正方形ABCD的顶点D关于射线CP的对称点G落在正方形内,连接BG并延长交边AD于点E,交射线CP于点F.连接DF,AF,CG.
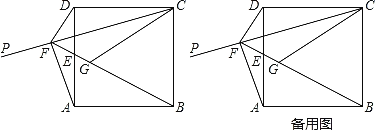
(1)试判断DF与BF的位置关系,并说明理由;
(2)若CF=4![]() ,DF=2,求AE的长;
,DF=2,求AE的长;
(3)若∠ADF=2∠FAD,求tan∠FAD的值.
【答案】(1)DF⊥BF,见解析;(2)![]() ;(3)2﹣
;(3)2﹣![]()
【解析】
(1)由轴对称的性质可得CD=CG,DF=FG,由“SSS”可证△CDF≌△CGF,可得∠CDF=∠CGF,由等腰三角形的性质和四边形内角和定理可求∠DFB=90°,可得结论;
(2)过点C作CH⊥BF于H,由等腰直角三角形的性质可求CH=FH=4,由勾股定理可求CG=BC=CD=2![]() ,通过证明△AEB∽△HBC,可得
,通过证明△AEB∽△HBC,可得![]() ,即可求解;
,即可求解;
(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,由题意可证点D、F、A、B四点共圆,可得∠DBF=∠DAF,∠FDA=∠FBA,可求∠FDA=30°,∠FAD=15°,利用锐角三角函数即可求解.
解:(1)DF⊥BF,
理由如下:
∵点D关于射线CP的对称点G,
∴CD=CG,DF=FG,
又∵CF=CF,
∴△CDF≌△CGF(SSS),
∴∠CDF=∠CGF,
∵CD=CB=CG,
∴∠CGB=∠CBG,
∵∠CGB+∠CGF=180°,
∴∠CBG+∠CDF=180°,
∵∠CDF+∠DFB+∠CBF+∠DCB=360°,
∴180°+90°+∠DFB=360°,
∴∠DFB=90°,
∴DF⊥BF;
(2)如图,过点C作CH⊥BF于H,
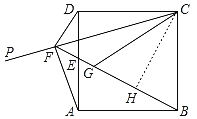
∵△CDF≌△CGF,∠DFB=90°,
∴∠CFD=∠CFG=45°,DF=FG=2,
∵CH⊥BF,
∴∠CFH=∠FCH=45°,
∴CH=FH,
∴CF=![]() CH=4
CH=4![]() ,
,
∴CH=FH=4,
∴GH=FH﹣FG=2,
∴CG![]() ,
,
∴CD=CG=BC=AB=![]() ,
,
∵CB=CG,CH⊥BG,
∴BH=GH=2,
∵AD∥BC,
∴∠AEB=∠CBH,
又∵∠DAB=∠CHB=90°,
∴△AEB∽△HBC,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ;
;
(3)连接BD,过点F作FM⊥AD于M,作∠AFN=∠FAD,交AD于N,

∵四边形ABCD是正方形,
∴∠ABD=∠ADB=45°,
∵∠DFB=∠DAB=90°,
∴点D、F、A、B四点共圆,
∴∠DBF=∠DAF,∠FDA=∠FBA,
∵∠ABD=∠FBD+∠FBA=∠FDA+∠DAF=45°,∠ADF=2∠FAD,
∴∠FDA=30°,∠FAD=15°,
∵∠AFN=∠FAD=15°,
∴∠FNM=30°,
又∵FM⊥AD,
∴NM=![]() FM,FN=2MF=AN,
FM,FN=2MF=AN,
∴AM=AN+MN=(2+![]() )FM,
)FM,
∴tan∠FAD=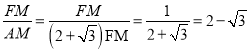 .
.

 习题精选系列答案
习题精选系列答案