题目内容
【题目】如图,在△ABF中,BE⊥AF垂足为E,AD∥BC,且AF平分∠DAB,求证:(1)FC=AD;(2)AB=BC+AD.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据平行线性质得到∠DAF=∠F,根据角平分线定义得到∠BAF=∠DAF,进而得到∠F=∠BAF,根据等角对等边得到AB=BF,根据等腰三角形三线合一得到AE=EF,利用ASA证得ADE≌△FCE,即可得证;
(2)由(1)中三角形全等可知AB=BF,AD=FC,利用等量代换即可解决问题.
(1)证明:∵AD∥BC
∴∠DAF=∠F
∵AF平分∠DAB
∴∠BAF=∠DAF
∴∠F=∠BAF
∴AB=BF
又 ∵BE⊥AF
∴AE=EF
在△ADE和△FCE中
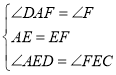
∴△ADE≌△FCE(ASA)
∴FC=AD
(2)证明:∵AB=BF AD=FC
又∵BF=BC+CF
∴AB=BC+AD

练习册系列答案
相关题目
【题目】某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
分组/元 | 频 数 | 频 率 |
1000<x<1200 | 3 | 0.060 |
1200<x<1400 | 12 | 0.240 |
1400<x<1600 | 18 | 0.360 |
1600<x<1800 | a | 0.200 |
1800<x<2000 | 5 | b |
2000<x<2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表a= ,b= ,和频数分布直方图;
(2)这50个家庭电费支出的中位数落在哪个组内?
(3)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭?







