题目内容
【题目】以四边形ABCD的边AB，AD为边分别向外侧作等边三角形ABF和等边三角形ADE，连接EB，FD，交点为G．
（1）当四边形ABCD为正方形时，如图①，EB和FD的数量关系是 ；
（2）当四边形ABCD为矩形时，如图②，EB和FD具有怎样的数量关系？请加以证明；
（3）如图③，四边形ABCD由正方形到矩形再到一般平行四边形的变化过程中，EB和FD具有怎样的数量关系？请直接写出结论，无需证明．
【答案】（1）DF＝BE；（2）EB＝FD，证明见解析；（3）DF＝BE
【解析】
（1）根据题意可得AB=AF，AD=AE，∠FAB=∠EAD，即可得∠FAD=∠EAB，则可证△AFD≌△AEB，可得BE=DF
（2）根据题意可得AB=AF，AD=AE，∠FAB=∠EAD，即可得∠FAD=∠EAB，则可证△AFD≌△AEB，可得BE=DF
（3）根据题意可得AB=AF，AD=AE，∠FAB=∠EAD，即可得∠FAD=∠EAB，则可证△AFD≌△AEB，可得BE=DF．
解：（1）∵四边形ABCD是正方形
∴AB＝AD，∠BAD＝90°
∵△BAF和△AED是等边三角形
∴AF＝AB，AD＝AE，∠FAB＝∠EAD＝60°
∴AE＝AD＝AF＝AB，∠FAD＝∠EAB
∴△ABE≌△ADF
∴DF＝BE
故答案为DF＝BE
（2）EB＝FD
理由如下：
∵△BAF和△AED是等边三角形
∴AF＝AB，AD＝AE，∠FAB＝∠EAD＝60°
∴∠FAB+∠BAD＝∠EAD+∠BAD
∴∠FAD＝∠EAB
又∵AF＝AB，AE＝AD
∴△ABE≌△AFD
∴DF＝BE
（3）BE＝DF
理由如下∵△BAF和△AED是等边三角形
∴AF＝AB，AD＝AE，∠FAB＝∠EAD＝60°
∴∠FAB+∠BAD＝∠EAD+∠BAD
∴∠FAD＝∠EAB
又∵AF＝AB，AE＝AD
∴△ABE≌△AFD
∴DF＝BE
【题目】如图，正方形
内部有若干个点，用这些点以及正方形的顶点
、
、
、
把原正方形分割成一些三角形（互相不重叠）
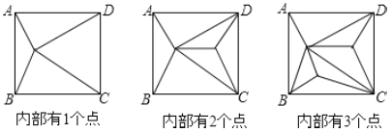
（1）填写下表：
正方形 | 1 | 2 | 3 | 4 | … |
|
分割成的三角形的个数 | 4 | 6 | ______ | ______ | … | ______ |
（2）如果原正方形内有101个点，此时原正方形被分割成多少个三角形？
【题目】某书店准备购进甲、乙两种图书共100本，购书款不高于2224元，预这100本图书全部售完的利润不低于1100元，两种图书的进价、售价如表所示：
甲种图书 | 乙种图书 | |
进价（元/本） | 16 | 28 |
售价（元/本） | 26 | 40 |
请回答下列问题：
（1）书店有多少种进书方案？
（2）在这批图书全部售出的条件下，（1）中的哪种方案利润最大？最大利润是多少？（请你用所学的函数知识来解决）
