题目内容
已知两圆的圆心分别在(2,0)、(0,2),半径都是2.则两圆公共部分的面积是______.
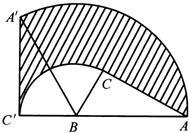
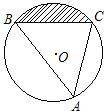
如图,
∵B(2,0)、C(0,2),半径都是2,
∴△OBC为等腰直角三角形,
∴∠OBC=45°,
而OA⊥BC,
∴∠AOB=45°,
∴△BAO为等腰直角三角形,
则S弓形OA=S扇形BOA-S△BAO=
-
×2×2=π-2.
所以两圆公共部分的面积=2S弓形OA=2π-4.
故答案为2π-4.

∵B(2,0)、C(0,2),半径都是2,
∴△OBC为等腰直角三角形,
∴∠OBC=45°,
而OA⊥BC,
∴∠AOB=45°,
∴△BAO为等腰直角三角形,
则S弓形OA=S扇形BOA-S△BAO=
| 90π×22 |
| 360 |
| 1 |
| 2 |
所以两圆公共部分的面积=2S弓形OA=2π-4.
故答案为2π-4.


练习册系列答案
相关题目