题目内容
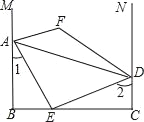
【题目】提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
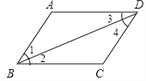
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180-∠A,∠2+∠4=180―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(_____)
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
【答案】 (1)答案见解析;(2)两组对角分别相等的四边形是平行四边形; (3)B
【解析】试题分析:(1)利用四边形的内角和和已知条件中的对角相等得到邻角互补,从而判定两组对边平行,进而证得结论;(2)两组对角分别相等的四边形是平行四边形;(3)由(1)即可得出结论.
解:(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=∠3.
正确证明:因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C,∠ABC=∠ADC,所以2∠A+
2∠ABC=360°.所以∠A+∠ABC=180°.所以AD∥BC.同理∠A+∠ADC=180°.所以AB∥CD.所以四边形ABCD是平行四边形.
(2)两组对角分别相等的四边形是平行四边形
(3)∵两组对角分别相等的四边形是平行四边形,
∴B正确.