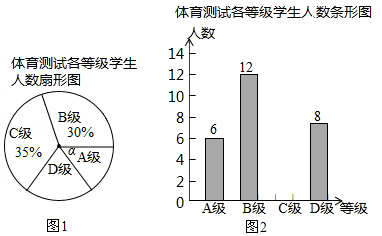
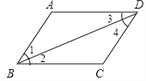
题目内容
【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值其中结论正确的有( )
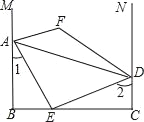
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:先根据AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,∠EAM和∠EDN的平分线交于点F,由三角形内角和定理以及平行线的性质即可得出结论.
详解:如图:
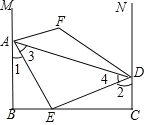
∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=12×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°90°=45°,
∴∠F=180°(∠FAD+∠FDA)=180°45°=135°,故④正确.
故选:C.

练习册系列答案
相关题目