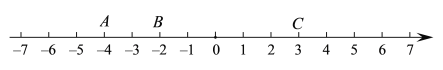题目内容
【题目】如图，已知数轴上的点A对应的数为6，B是数轴上的一点，且AB=10，动点P从点A出发，以每秒6个单位长度的速度沿着数轴向左匀速运动，设运动时间为t秒(t>0).
(1)数轴上点B对应的数是________，点P对应的数是_________(用t的式了表示)；
(2)动点Q从点B与点P同时发，以每秒4个单位长度的速度沿着数轴向左匀速运动，试问：运动多少时间点P可以追上点Q?
【答案】（1）-4；6-6t;（2）5秒.
【解析】
（1）根据A点对应的数为6，B是数轴上的一点，且AB=10，可得B点对应的数为：6-10=-4；点P表示的数为：6-6t；
（2）点P运动x秒时，在点C出追上点Q，然后建立方程6x-4x=10，解方程即可.
（1）有题意可得：
B点表示的数为：6-10=-4；
点P表示的数为：6-6t；
故答案为：-4,6-6t;
（2）设点P运动x秒时，在点C处追上点Q（如下图）
则AC=6x,BC=4x,
由AC-BC=AB可得：
解得：
所以点P运动5秒时，在点C处追上点Q.
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
