Question

【题目】已知，抛物线C1：

(1) ① 无论m取何值，抛物线经过定点P

② 随着m的取值的变化，顶点M(x，y)随之变化，y是x的函数，则点M满足的函数C2的关系式为__________________

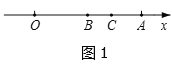
(2) 如图1，抛物线C1与x轴仅有一个公共点，请在图1画出顶点M满足的函数C2的大致图象，平行于y轴的直线l分别交C1、C2于点A、B．若△PAB为等腰直角三角形，判断直线l满足的条件，并说明理由

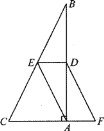
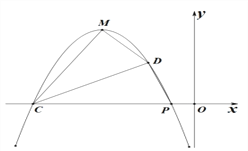
(3) 如图2，二次函数的图象C1的顶点M在第二象限、交x轴于另一点C，抛物线上点M与点P之间一点D的横坐标为－2，连接PD、CD、CM、DM．若S△PCD＝S△MCD，求二次函数的解析式

Answer 1

【答案】（1）①（－1，0 ）②；（2）详见解析；（3）详见解析.

【解析】试题分析：（1）①直接得出点的坐标；②用配方法确定出抛物线的顶点式方程，即可得出结论
（2）先确定出抛物线的解析式，得出此两个函数图形关于轴对称，从而设出点的坐标，最后利用等腰直角三角形的性质列出方程，解方程即可得出结论；
（3）方法一：先确定出点坐标，根据条件确定出四边形的面积是面积的2倍，列出方程即可确定出．最后代入解析式即可；
方法二：先确定出直线解析式，再用到坐标系下的三角形面积公式（水平宽乘以铅垂高的一半建立方程的）分别表示出和，从而建立方程求解，再代入解析式即可．

试题解析：(1)①∵抛物线

∴当x+1=0时，无论m为何值，抛物线经过顶点P，

∴x=1，y=0，

∴定点P(1,0)，

故答案为：1，0；

②抛物线

∴

∴函数的关系式为

故答案为：

(2)如图1所示，

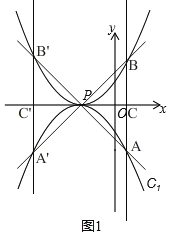
∵抛物线顶点在x轴，则m=1，

∴抛物线 P(1,0)，

由②知,函数的关系式为

∴抛物线与关于x轴对称，

∵△PAB为等腰直角三角形，

∴直角顶点只能是点P，且PC=BC=AC，

设

∴ ∴PC=|n+1|，

∴ ∴n=1(舍)或n=1或n=3.

∴直线l的解析式为x=1或x=3.

(3)方法一：如图2，过点M作ME⊥OC，过点D作DF⊥OC，

∵抛物线

∴P(1,0),C(2m+1,0)，

∵抛物线上点M与点P之间一点D的横坐标为2，

∴

∴

∵

S四边形CPDM=S△DFP+S梯形DFEM+S△CEM

∴PF×DF+EF×DF+ME×EF+CE×ME=2PC×DF，

∴DF(PF+EF)+ME(EF+CE)=2PC×DF，

∴DF×PE+ME×CF=2PC×DF，

∴DF×12PC+ME(PCPF)=2PC×DF，

∴DF×PC+2ME×PC2ME×PF=4PC×DF，

∴2ME×PC3PC×DF=2ME×PF，

∴PC(2ME3DF)=2ME×PF，

∴(m+1)(m+4)(2m+3)=0，

∴m=1(舍)或m=4或

当m=4时,二次函数的解析式

当时,二次函数的解析式

方法二，如图，过点M作ME⊥x轴交CD于E，过点D作DF⊥x轴，

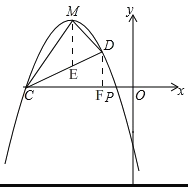
∵抛物线

∴P(1,0),C(2m+1,0)，

∵抛物线上点M与点P之间一点D的横坐标为2，

∴

∴直线CD解析式为

∴

∵

∴(m+1)(m+4)(2m+3)=0，

∴m=1(舍)或m=4或

当m=4时,二次函数的解析式

当时,二次函数的解析式