Question

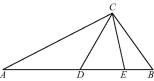
【题目】如图，等边三角形的边长为，是边上的高所在的直线，点为直线上的一动点，连接并将绕点逆时针旋转至，连接，则的最小值为________．

Answer 1

【答案】

【解析】

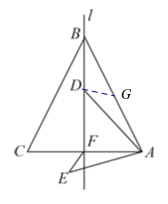
取AB的中点G，连接DG.先根据条件证明△ADG≌△AEF，从而EF=DG，根据“垂线段最短”可得，当DG⊥AB时，DG最短，再利用勾股定理在Rt△BGD中，求出DG即可.

解：如图，取AB的中点G，连接DG.

∵旋转角为60°，

∴ ∠DAE=60°，

∵∠BAC=60°，

∴∠GAD=∠BAC -∠DAC=60°-∠DAC,

∠FAE=∠DAE-∠DAF=60°-∠DAC,

∴∠GAD=∠FAE，

∵BF为等边三角形ABC的高，

∴ AF=AC,（等腰三角形三线合一），

∴AG=AF,

∵AE由AD旋转可得，

∴AD=AE,

在△ADG和△AEF中，

,

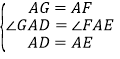∴△ADG≌△AEF，

∴EF=DG,

∴ 当DG⊥AB时，EF最短，

∵∠ABF=∠ABC=30°，BG=×6=3.

∴BD=2DG,(直角三角形中30°角所对的边是斜边的一半)，

在Rt△BGD中，

,

∴ 4DG2=DG2+9,

∴ DG= ,

∴ EF的最小值为.

故答案为：.