Question

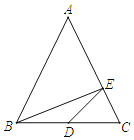
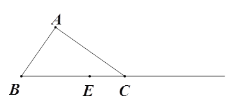
【题目】如图，在△ABC中，AB=，AC=，BC=3，将△ABC沿射线BC平移，使边AB平移到DE，得到△DEF.

(1)作出平移后的△DEF(要求：尺规作图，保留作图痕迹，不写作法)；

(2)若AC、DE相交于点H，BE=2，求四边形DHCF的面积.

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）根据“已知三边作三角形”即可得解；

（2）根据题意得△ABC是直角三角形，易得其面积，再证明△ECH∽△EFD得＝，从而得四边形DHCF的面积＝S△DE，即可得解.

（1）作图如图所示：

（2）∵AB=，AC=，BC=3，

∴BC2=AB2+AC2，

∴△ABC是直角三角形，

∴S△DEF＝S△ABC＝··＝

∵EF＝BC＝3，BE＝2

∴EC＝BC－BE＝1

∵ AC∥DF

∴△ECH∽△EFD

∴＝＝

∴四边形DHCF的面积＝S△DEF＝· ＝