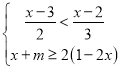题目内容
【题目】如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数y=﹣![]() x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣
x2+bx+c的图象经过A、E两点,且点E的坐标为(﹣![]() ,0),以0C为直径作半圆,圆心为D.
,0),以0C为直径作半圆,圆心为D.
(1)求二次函数的解析式;
(2)求证:直线BE是⊙D的切线;
(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.
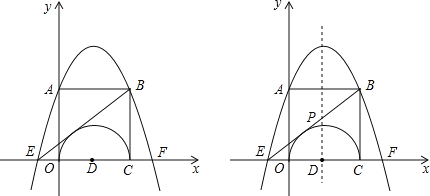
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,S存在最大值,当t=1时,S最大=
,S存在最大值,当t=1时,S最大=![]() .
.
【解析】
(1)利用待定系数法,根据题意易得点A、B的坐标,然后把点A、B、E的坐标分别代入二次函数解析式,列出关于a、b、c的方程组,利用三元一次方程组来求得系数的值;
(2)过点D作DG⊥BE于点G,构建相似三角形△EGD∽△ECB,根据它的对应边成比例得DG的值,利用待定系数法求得直线BE的解析式,由此求得DG=1(圆的半径是1),则易证得结论;
(3)由(2)中可求得点P的坐标,由相似三角形△MNC∽△BEC的对应边成比例,线段间的和差关系得到CN、DN的值,由题可得S=S△PND+S梯形PDCMS△MNC,再结合抛物线的性质可求得S的最值.
解:(1)由题意,得A(0,2),点B(2,2),E的坐标为(![]() ,0)
,0)
则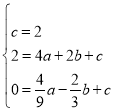 ,解得
,解得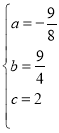
故二次函数的解析式为:![]() ;
;
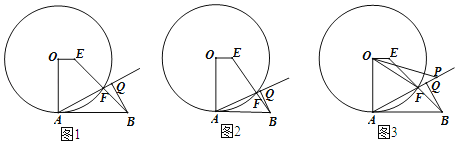
(2)如图1,过点D作DG⊥BE于点G,
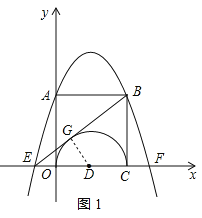
由题意,得
ED=![]() ,EC=
,EC=![]() ,BC=2
,BC=2
∴BE=![]()
∵∠BEC=∠DEG,∠EGD=∠ECB=90°
∴△EGD∽△ECB
∴![]() ,
,
∴DG=1
∵圆D的半径为1,且DG⊥BE
∴BE是圆D的切线
(3)如图2,过点M作MN∥BE交x轴与点N,连结PM,PN,
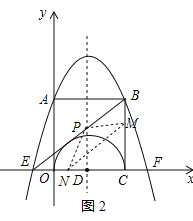
依题意,得,点B(2,2),E的坐标为(![]() ,0),
,0),
故设直线BE为y=kx+h(k≠0)
则有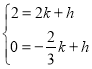 ,解得
,解得![]() ,
,
∴直线BE为:![]()
∵直线BE与抛物线的对称轴交点为P,对称轴为x=1
∴点P的纵坐标为y=![]() ,即P(1,
,即P(1,![]() )
)
∵MN∥BE
∴∠MNC=∠BEC
∵∠MCN=∠BCE=90°
∴△MNC∽△BEC
∴![]()
∴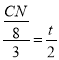 ,即
,即![]() ,
,
∴![]() ,
,
∴S△PND=![]()
S△MNC=![]()
S梯形PDCM=![]()
∴S=S△PND+S梯形PDCM﹣S△MNC=![]() (0<t<2)
(0<t<2)
∵抛物线S=![]() (0<t<2)的开口方向向下
(0<t<2)的开口方向向下
∴S存在最大值,当t=1时,S最大=![]() .
.

【题目】为了提高学生的身体素质,某班级决定开展球类活动,要求每个学生必须在篮球、足球、排球、乒乓球、羽毛球中选择一项参加训练(只选择一项),根据学生的报名情况制成如下统计表:
项目 | 篮球 | 足球 | 排球 | 乒乓球 | 羽毛球 |
报名人数 | 12 | 8 | 4 | a | 10 |
占总人数的百分比 | 24% | b |
(1)该班学生的总人数为 人;
(2)由表中的数据可知:a= ,b= ;
(3)报名参加排球训练的四个人为两男(分别记为A、B)两女(分别记为C、D),现要随机在这4人中选2人参加学校组织的校级训练,请用列表或树状图的方法求出刚好选中一男一女的概率.