Question

【题目】如图，扇形OAB中，∠AOB=60°，扇形半径为4，点C在上，CD⊥OA，垂足为点D，当△OCD的面积最大时，图中阴影部分的面积为_____．

Answer 1

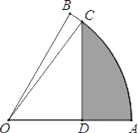
【答案】2π－4

【解析】

由OC＝4，点C在上，CD⊥OA，求得DC＝＝，运用S△OCD＝OD，求得OD＝时△OCD的面积最大，运用阴影部分的面积＝扇形AOC的面积－△OCD的面积求解．

∵OC＝4，点C在上，CD⊥OA，∴DC＝＝，∴S△OCD＝OD，∴S△OCD2＝OD2（16－OD2）＝－OD4＋4OD2＝－（OD2－8）2＋16，∴当OD2＝8，即OD＝2时△OCD的面积最大，∴DC＝＝＝2，∴∠COA＝45°，∴阴影部分的面积＝扇形AOC的面积－△OCD的面积＝－4＝2π－4，故答案为2π－4.