题目内容
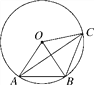
【题目】如图,已知点A,B,C在⊙O上,且点B是的中点,当OA=5cm,cos∠OAB=![]() 时.
时.
(1)求△OAB的面积;
(2)连接AC,求弦AC的长.
【答案】(1)12cm2;(2)![]() cm.
cm.
【解析】试题分析:(1)过O作OH⊥AB于H.,利用垂径定理,构造直角三角形,求出OH,AB, 求得△OAB的面积.(2) 设AC交OB于M.,利用三角函数求出AB=BC,OB垂直平分AC,可求得AC.
试题解析:
解:(1)过O作OH⊥AB于H.∵OA=5cm,cos∠OAB=![]() ,
,
∴AH=OA·cos∠OAB=3cm,
∴OH=4cm,AB=2AH=6cm,∴S△OAB=![]() AB·OH=12cm2;
AB·OH=12cm2;
(2)设AC交OB于M.∵OA=OB,
∴∠OBA=∠OAB,∴sin∠OBA=![]() .
.
∵B是弧AC的中点,∴弧AB=弧BC,
∴AB=BC.∵OA=OC,∴OB垂直平分AC.
∴AM=AB·sin∠MBA=6×![]() =
=![]() (cm),∴AC=2AM=
(cm),∴AC=2AM=![]() cm.
cm.

练习册系列答案
相关题目