Question

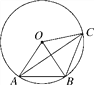
【题目】如图，AB是⊙O的切线，B为切点，圆心O在AC上，∠A＝30°，D为的中点．

(1)求证：AB＝BC；

(2)试判断四边形BOCD的形状，并说明理由．

Answer 1

【答案】（1）见解析；（2）四边形BOCD为菱形．

【解析】试题分析：(1) AB是⊙O的切线，利用圆半径构成的等腰三角形，得到∠OCB＝∠A, 从而AB＝BC.(2) 连接OD交BC于点M, OD垂直平分BC,OC=OD,OM=OD,可得四边形BOCD为菱形．

试题解析：

证明：∵AB是⊙O的切线，∴∠OBA＝90°，∠AOB＝90°－30°＝60°.∵OB＝OC，∠OBC＝∠OCB，

∴∠OCB＝∠AOB＝30°＝∠A，∴AB＝BC.

(2)解：四边形BOCD为菱形．理由如下：连接OD交BC于点M.

∵D是弧BC中点∴OD垂直平分BC.在Rt△OMC中，

∵∠OCM＝30°，∴OC＝2OM＝OD，∴OM＝MD，

∴四边形BOCD为菱形．