题目内容
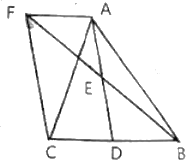
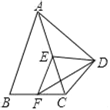
【题目】如图，在四边形ABCD中，∠ADC＝90°，AB＝AC，E，F分别为AC，BC的中点，连接EF，ED，FD．
（1）求证：ED＝EF；
（2）若∠BAD＝60°，AC平分∠BAD，AC＝6，求DF的长．
【答案】(1)见解析;(2)3
.
【解析】
（1）根据题意只要证明EF为△ABC的中位线，即可证明DE＝EF.
（2）只要证明
为直角三角形，根据勾股定理即可计算DF的长
（1）证明：∵∠ADC＝90°，E为AC的中点，
∴DE＝AE＝
AC．
∵E、F分别为AC、BC的中点，
∴EF为△ABC的中位线，
∴EF＝AB．
∵AB＝AC，
∴DE＝EF．
（2）解：∵∠BAD＝60°，AC平分∠BAD，
∴∠BAC＝∠DAC＝∠BAD＝30°．
由（1）可知EF∥AB，AE＝DE，
∴∠FEC＝∠BAC＝30°，∠DEC＝2∠DAC＝60°，
∴∠FED＝90°．
∵AC＝6，
∴DE＝EF＝3，
∴DF＝
＝3 ．
练习册系列答案
相关题目
【题目】将图1中的正方形剪开得到图2，则图2中共有4个正方形；将图2中的一个正方形剪开得到图3，图3中共有7个正方形；将图3中4个较小的正方形中的一个剪开得到图4，则图4中共有10个正方形，照这个规律剪下去：
（1）根据图中的规律补全表：
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
（2）第n个图形中有多少个正方形？
（3）当n=673时，图形中有多少个正方形？
