题目内容
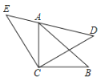
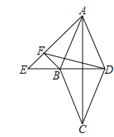
【题目】如图,点E在菱形ABCD的对角线DB的延长线上,且∠AED=45°,过B作AE的垂线交AE于F,连接FD.当∠AFD=60°时,![]() =___________
=___________
【答案】![]()
【解析】
首先作辅助线,延长FB交AC于点G,连接DG,因为∠AED=45°,BF⊥AE,得出∠EBF=45°,又因为菱形ABCD,得出∠GBD=∠GDB=∠EBF=45°,进而得出∠BGD=90°,BG=GD,又因为∠AFD=60°,得出∠DFG=30°,在Rt△FGD中,设BG=GD=x,FB+根据三角函数性质可得BG=![]() GD,进而得出FB=
GD,进而得出FB=![]() ,又△FEB∽△GDB,可得出
,又△FEB∽△GDB,可得出 ,即可得解.
,即可得解.
解:
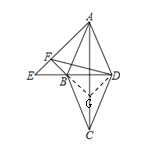
如图,延长FB交AC于点G,连接DG
∵∠AED=45°,BF⊥AE
∴∠EBF=45°
∵菱形ABCD,
∴∠GBD=∠GDB=∠EBF=45°
∴∠BGD=90°,BG=GD,
又∵∠AFD=60°
∴∠DFG=30°
在Rt△FGD中,设BG=GD=x
FB+BG=![]() GD
GD
∴FB=![]()
又△FEB∽△GDB
∴
故答案为![]() .
.

练习册系列答案
相关题目