题目内容
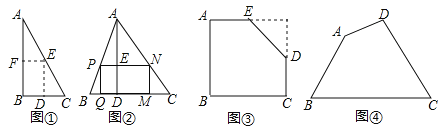
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 向点
向点![]() 运动,过点
运动,过点![]() 作
作![]() 交边
交边![]() 或边
或边![]() 于点
于点![]() ,点
,点![]() 是射线
是射线![]() 上的一点,且
上的一点,且![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).

(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值.
的值.
(3)当矩形![]() 与
与![]() 重叠部分图形为四边形时,求
重叠部分图形为四边形时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)点![]() 与点
与点![]() 同时出发,在线段
同时出发,在线段![]() 上以每秒2个单位长度的速度沿
上以每秒2个单位长度的速度沿![]() 往返运动,连结
往返运动,连结![]() 、
、![]() ,当点
,当点![]() 停止时点
停止时点![]() 也随之停止,直接写出矩形
也随之停止,直接写出矩形![]() 面积是
面积是![]() 面积的4倍时
面积的4倍时![]() 的值.
的值.
【答案】(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(2)
;(2)![]() ;(3)
;(3)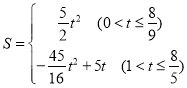 ;(4)t的值为
;(4)t的值为![]() 或
或![]() .
.
【解析】
(1)分两种情况:D在AC和BC上,根据三角函数列式先求PD的长,可得结论;
(2)如图4,根据EF=2BE,列方程可得结论;
(3)存在两种情况,先求边界点时t的值,分别画图根据面积公式可得结论;
(4)分两种情况,根据矩形PEFD面积是△QEF面积的4倍列方程可得t的值.
解:(1)∵∠C=90°,AC=4,BC=2,
∴AB=![]() ,
,
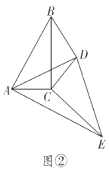
如图2,当D与C重合时,CP⊥AB,
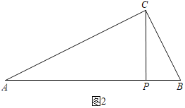
cos∠A=![]() ,
,
即![]() ,
,
AP=![]() ,
,
tan∠A=![]() ,
,
即![]() ,
,
∴PD=![]() ,
,
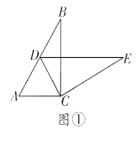
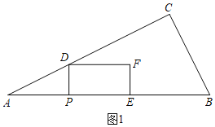
∴当0<t≤![]() 时,如图1,PE=2PD=2×
时,如图1,PE=2PD=2×![]() =
=![]() ,
,
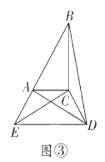
如图3,AP=![]() ,
,
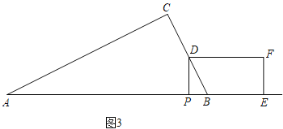
∴PB=![]() ,
,
tan∠DBP=![]() ,
,
即![]() ,
,
PD=![]() ,
,
当![]() <t≤2时,如图3,PE=2PD=2(
<t≤2时,如图3,PE=2PD=2(![]() )=
)=![]() ;
;
(2)当点F落在BC上时,如图4,
BE=![]() ,EF=PD=
,EF=PD=![]() ,
,
∵EF=2BE,
∴![]() =2×(
=2×(![]() ),
),
∴t=![]() (秒);
(秒);
(3)当0<t≤![]() 时,如图1,矩形PEFD与△ABC重叠部分图形是矩形PEFD,
时,如图1,矩形PEFD与△ABC重叠部分图形是矩形PEFD,
S=PDPE=![]() ;
;
如图5,当E与B重合时,PB=2PD,
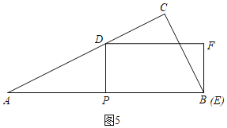
则![]() ,解得:t=1,
,解得:t=1,
当1<t≤![]() 时,如图6,
时,如图6,
cos∠A=![]() ,
,
即![]() ,
,
∴AD=![]() ,
,
∴CD=![]() ,
,
∵DM∥
∴∠CDM=∠A,
∴cos∠A=cos∠CDM=![]() ,
,
即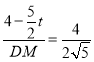 ,
,
∴DM=![]() ,
,
S=![]() ;
;
综上,S与t之间的函数关系式是: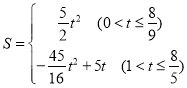 ;
;
(4)①当0<t≤1时,过Q作QH⊥AB于H,
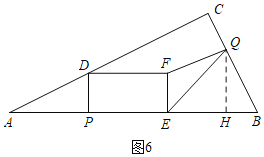
∵AP=![]() ,BQ=2t,
,BQ=2t,
∴PE=![]() ,PD=
,PD=![]() ,BH=
,BH=![]() ,
,
∴EH=BE![]() BH=
BH=![]() ,
,
∵矩形PEFD面积是△QEF面积的4倍,
∴![]() ,
,
解得:t=0(舍)或![]() ;
;
②当1<t≤2时,如图7,过Q作QH⊥AB于H,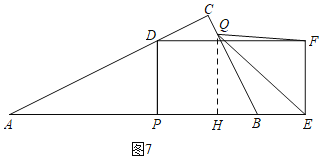
∵PE=![]() ,PB=
,PB=![]() ,
,
∴BE=PE![]() PB=
PB=![]() ,
,
∵BQ+CQ=2t,
∴BQ=4-2t,
∴BH=![]() ,
,
∵矩形PEFD面积是△QEF面积的4倍,
∴![]() ,
,
t=0(舍)或![]() ;
;
综上,t的值是![]() 秒或
秒或![]() 秒.
秒.

【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
【题目】今年4月份,某校九年级学生参加了广州市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
分组 | 分数段(分) | 频数 |
|
| 2 |
|
| 5 |
|
| 15 |
|
|
|
|
| 10 |
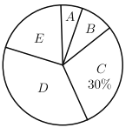
(1)求全班学生人数和![]() 的值.
的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3