Question

若弓形的弦长为4，弓形的高为1，那么弓形所在圆的半径．

Answer 1

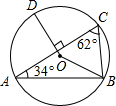
设弓形所在圆O的半径为r，过点O作AB的垂线OD，垂足为C，交⊙O于D，则∠ACO=90°．
∵AB=4，
∴AC=

1

2

AB=2．
在Rt△AOC中，OA=r，OC=r-1，AC=2，
由勾股定理，得OC²+AC²=OA²，
即（r-1）²+2²=r²，
解得：r=2.5
故弓形所在圆的半径为2.5．