题目内容
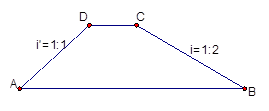
（9分）如图，流经某市的一条河流的两岸互相平行，河岸l1上有一排观赏灯，已知相邻两灯之间的距离AB=60米，某人在河岸l2的C处测得∠ACE=60°,然后沿河岸向右走了140米到达D处，测得∠BDE=30°．求河流的宽度AE（结果保留三个有效数字，参考数据：
）．
）．解：过点A作AF∥BD交l2于点F.
∵l1∥l2，AF∥DB，
∴四边形AFDB是平行四边形.
∴DF=AB=60,∠AFC=30°，
∴CF=CD－DF=140－60=80.…（3分）
又∵∠ACE是△ACF的一个外角，
∴∠CAF=∠ACE－∠AFC=60°－30°=30°，
∴∠CAF=∠AFC.
∴AC=CF="80." ……………………………………………………………（6分）
在Rt△AEC中，∠ACE=60°
∴AE=AC·sin60°=80×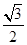
≈69.28≈69.3（米）…………………………（8分）
答：河流的宽度AE约为69.3米.
∵l1∥l2，AF∥DB，
∴四边形AFDB是平行四边形.
∴DF=AB=60,∠AFC=30°，
∴CF=CD－DF=140－60=80.…（3分）
又∵∠ACE是△ACF的一个外角，
∴∠CAF=∠ACE－∠AFC=60°－30°=30°，
∴∠CAF=∠AFC.
∴AC=CF="80." ……………………………………………………………（6分）
在Rt△AEC中，∠ACE=60°
∴AE=AC·sin60°=80×
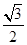≈69.28≈69.3（米）…………………………（8分）答：河流的宽度AE约为69.3米.
略
练习册系列答案
相关题目
的正方形网格中，每个小正方形的边长
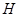点，并测得HB=6m．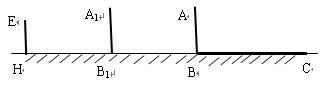
在图中画出形成影子的光线，并确定路灯灯泡所在的位置G；
点出发，他们在岸边跑的速度都是5米/秒，在水中游泳的速度都是2米/秒，∠BAD=45°，请你通过计算说明谁先到达营救地点
．
≈1.414，
≈1.732）．
）m
