题目内容
如图，水坝的横断面，坝顶宽3m，坝高4m，迎水坡坡度i=1:2, 背水坡坡度I’=1:1，∠A=________;坡底AB=__________
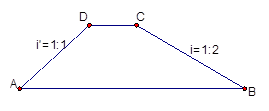
分析：根据已知背水坡的坡度i′可求得∠A的度数；
过点C作CF⊥AB于F，从而得到DC=EF，DE=CF，再根据坡度求得BF的长，这样就不难求出AB的长．
解答：
解：过点C作CF⊥AB于F．
因为tanA=
=1：1，即AE=DE，AE⊥DE，
∴∠A=45°；
∵DE⊥AE，DC∥AB，
∴四边形EFCD为矩形，
∴DE=CF=4米，CD=EF=3米，
∵tanB=
，
∴BF=2CF=8米，
∴AB=DE+DC+BF=4+3+8=15米．
故答案为45°，15m．
过点C作CF⊥AB于F，从而得到DC=EF，DE=CF，再根据坡度求得BF的长，这样就不难求出AB的长．
解答：
解：过点C作CF⊥AB于F．因为tanA=
=1：1，即AE=DE，AE⊥DE，∴∠A=45°；
∵DE⊥AE，DC∥AB，
∴四边形EFCD为矩形，
∴DE=CF=4米，CD=EF=3米，
∵tanB=
，∴BF=2CF=8米，
∴AB=DE+DC+BF=4+3+8=15米．
故答案为45°，15m．
练习册系列答案
相关题目
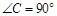，AB的垂直平分线与BC，AB的交点分别为D，E．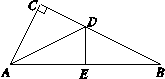
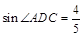，求AC的长和
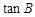的值；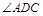
=
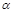，参考（1）的计算过程直接写
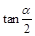的值（用
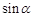和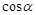
的值表示）．
）．
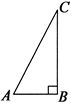
＋(1－tanB)2＝0，求∠C的度数
，则这个三角形是 
中，
D是BC上的点，
.求AC(
，结果保留整数).
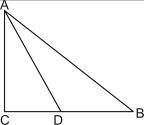
； ②