题目内容
已知一个二次函数的关系式为 y=x2-2bx+c.
(1)若该二次函数的图象与x轴只有一个交点,
①则b、c 应满足关系为 ;
②若该二次函数的图象经过A(m,n)、B(m +6,n)两点,求n的值;
(2)若该二次函数的图象与x轴有两个交点C(6,0)、D(k,0),线段CD(含端点)上有若干个横坐标为整数的点,且这些点的横坐标之和为21,求b的取值范围.
(1)若该二次函数的图象与x轴只有一个交点,
①则b、c 应满足关系为 ;
②若该二次函数的图象经过A(m,n)、B(m +6,n)两点,求n的值;
(2)若该二次函数的图象与x轴有两个交点C(6,0)、D(k,0),线段CD(含端点)上有若干个横坐标为整数的点,且这些点的横坐标之和为21,求b的取值范围.
(1)c=b2,9;(2)7≤b<7.5或2.5<b≤3.5.
试题分析:(1)①根据二次函数的图象与x轴只有一个交点,则b2-4ac=0,由此可得到b、c 应满足关系;
②把A(m,n)、B(m+6,n)分别代入抛物线的解析式,再根据①的结论即可求出n的值;
(2)因为y=x2-2bx+c图象与x轴交于C(6,0),即可得到36-12b+c=0,所以c=12b-36,进而得到k=2b-6,再根据C、D之间的整数和为21,即可求出b的取值范围.
(1)①∵二次函数的图象与x轴只有一个交点,
∴b2-4ac=0,
∴c=b2,
②由
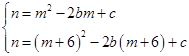 ,
,得b=m+3,则c=(m+3)2;
于是,n=m2-2(m+3)m+(m+3)2=9;
(2)∵y=x2-2bx+c图象与x轴交于C(6,0)
∴36-12b+c=0,∴c=12b-36
∴y=x2-2bx+12b-36,
令y=0得x2-2bx+12b-36=0
解得:x1=6,x2=2b-6,即k=2b-6;
∵C、D之间的整数和为21,
∴由8≤k<9,或-1<k≤1,
∴8≤2b-6<9,或-1<2b-6≤1,
解得7≤b<7.5或2.5<b≤3.5.

练习册系列答案
相关题目
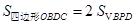 ;
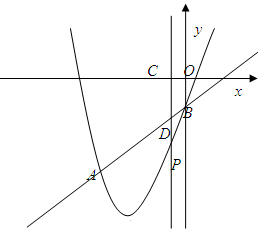
;
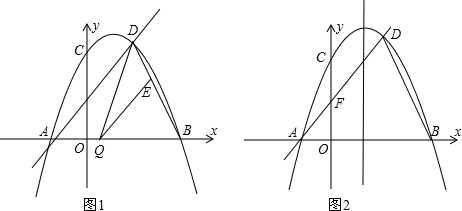

 的一元二次方程
的一元二次方程 .
. 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.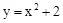 向下平移3个单位,那么所得新抛物线的表达式是 .
向下平移3个单位,那么所得新抛物线的表达式是 .
 ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。