题目内容
已知直角坐标系中有一点A(-4,3),点B在x轴上,△AOB是等腰三角形。
(1)求满足条件的所有点B的坐标。(直接写出答案)
(2)求过O、A、B三点且开口向下的抛物线的函数解析式。(只需求出满足条件的即可)。
(3)在(2)中求出的抛物线上存在点p,使得以O、A、B、P四点为顶点的四边形是梯形,求满足条件的所有点P的坐标及相应梯形的面积。

(1)求满足条件的所有点B的坐标。(直接写出答案)
(2)求过O、A、B三点且开口向下的抛物线的函数解析式。(只需求出满足条件的即可)。
(3)在(2)中求出的抛物线上存在点p,使得以O、A、B、P四点为顶点的四边形是梯形,求满足条件的所有点P的坐标及相应梯形的面积。

(1)(-5,0);(5,0);(-8,0);(-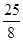 ,0).(2) 当AB=OA时,y=-
,0).(2) 当AB=OA时,y=- x2-
x2-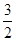 x;当OA=OB时,同理得y=-
x;当OA=OB时,同理得y=-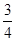 x2-
x2-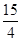 x;(3) (4,-9),48.(-12,-9),48. (1,-
x;(3) (4,-9),48.(-12,-9),48. (1,-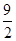 ),
), .(-9,-27),75.
.(-9,-27),75.
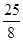 ,0).(2) 当AB=OA时,y=-
,0).(2) 当AB=OA时,y=- x2-
x2-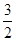 x;当OA=OB时,同理得y=-
x;当OA=OB时,同理得y=-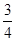 x2-
x2-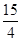 x;(3) (4,-9),48.(-12,-9),48. (1,-
x;(3) (4,-9),48.(-12,-9),48. (1,-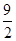 ),
), .(-9,-27),75.
.(-9,-27),75.试题分析:(1)根据点A的坐标,易求得OA=5,若△AOB是等腰三角形,应分三种情况考虑:
①OA=OB=5,由于点B的位置不确定,因此要分B在x轴正、负半轴两种情况求解,已知了OB的长,即可得到点B的坐标;
②OA=AB=5,此时点B只能在x轴负半轴上,那么点B的横坐标应为点A横坐标的2倍,可据此求得点B的坐标;
③AB=OB=5,此时点B只能在x轴负半轴上,可在x轴上截取AD=OA,通过构建相似三角形:△OBA∽△OAD,通过所得比例线段来求出OB的长,从而得到点B的坐标.
(2)任选一个(1)题所得的B点坐标,利用待定系数法求解即可.
(3)解此题时,虽然不同的抛物线有不同的解,但解法一致;分两种情况:
①OA∥BP时,可分别过A、P作x轴的垂线,设垂足为C、E,易证得△AOC∽△PBE,根据所得比例线段,即可求得点P的坐标.而梯形ABPO的面积可化为△ABO、△PBO的面积和来求出.
②OP∥AB时,方法同上,过P作PF⊥x轴于F,然后通过相似三角形:△ABC∽△POF,来求出P点坐标,梯形面积求法同上.(当OA=AB时,两种情况的点P正好关于抛物线对称轴对称,可据此直接求出P点坐标,避免重复计算.)
作AC⊥x轴,由已知得OC=4,AC=3,OA=
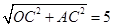
(1)当OA=OB=5时,
如果点B在x轴的负半轴上,如图(1),点B的坐标为(-5,0);
如果点B在x轴的正半轴上,如图(2),点B的坐标为(5,0);
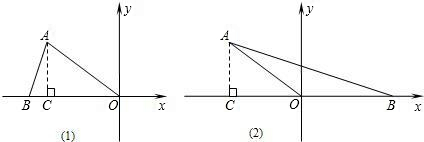
当OA=AB时,点B在x轴的负半轴上,如图(3),BC=OC,则OB=8,点B的坐标为(-8,0);
当AB=OB时,点B在x轴的负半轴上,如图(4),在x轴上取点D,使AD=OA,可知OD=8.

由∠AOB=∠OAB=∠ODA,可知△AOB∽△ODA,
则
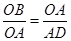 ,
,解得OB=
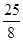 ,
,点B的坐标为(-
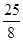 ,0).
,0).(2)当AB=OA时,抛物线过O(0,0),A(-4,3),B(-8,0)三点,
设抛物线的函数表达式为y=ax2+bx,
可得方程组
 ,
,解得
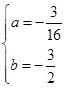 ,
,∴y=-
 x2-
x2-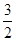 x;
x;当OA=OB时,同理得y=-
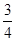 x2-
x2-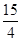 x;
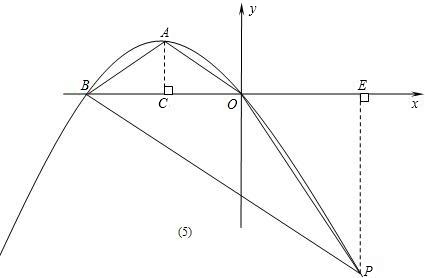
x;(3)当OA=AB时,若BP∥OA,如图(5),作PE⊥x轴,
则∠AOC=∠PBE,∠ACO=∠PEB=90°,
∴△AOC∽△PBE,
∴
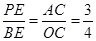 .
.设BE=4m,PE=3m,则点P的坐标为(4m-8,-3m),
代入y=-
 x2-
x2- x,
x,解得m=3;
则点P的坐标为(4,-9),
S梯形ABPO=S△ABO+S△BPO=48.
若OP∥AB,根据抛物线的对称性可得点P的坐标为(-12,-9),
S梯形AOPB=S△ABO+S△BPO=48.
当OA=OB时,若BP∥OA,如图(6),作PF⊥x轴,
则∠AOC=∠PBF,∠ACO=∠PFB=90°,
△AOC∽△PBF,
 ;
;设BF=4m,PF=3m,则点P的坐标为(4m-5,-3m),
代入y=-
 x2-
x2- x,
x,解得m=
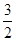 .则点P的坐标为(1,-
.则点P的坐标为(1,-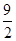 ),
),S梯形ABPO=S△ABO+S△BPO=
 .
.若OP∥AB(图略),作PF⊥x轴,
则∠ABC=∠POF,∠ACB=∠PFO=90°,
△ABC∽△POF,
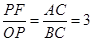 ;
;设点P的坐标为(-n,-3n),
代入y=-
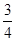 x2-
x2-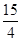 x,
x,解得n=9.
则点P的坐标为(-9,-27),S梯形AOPB=S△ABO+S△BPO=75.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
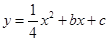 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线 于点C;
于点C; 的坐标,判定点
的坐标,判定点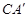 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.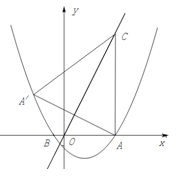
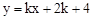 与抛物线
与抛物线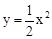 交于A、B两点,
交于A、B两点,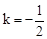 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;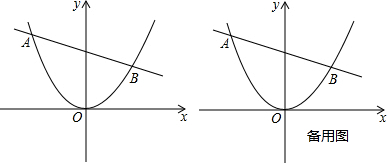
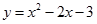 的图象如图所示.当y<0时,自变量x的取值范围是( ).
的图象如图所示.当y<0时,自变量x的取值范围是( ).
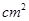 ),则s(
),则s(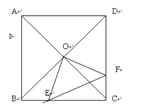
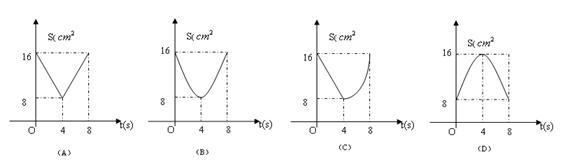

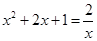 的正数根的个数为( )
的正数根的个数为( )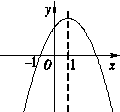

 时,y随x的增大而增大
时,y随x的增大而增大
 是一元二次方程
是一元二次方程 的一个根
的一个根