题目内容
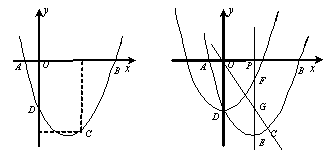
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。

 ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
| A.①② | B.③④ | C.①④ | D.①③ |
D.
试题分析:①∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),对称轴直线是x=1,
∴该抛物线与x轴的另一个交点的坐标是(3,0),
∴根据图示知,当x>3时,y<0.
故①正确;
②根据图示知,抛物线开口方向向下,则a<0.
∵对称轴x=-
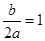
∴b=-2a,
∴3a+b=3a-2a=a<0,即3a+b<0.
故②错误;
③∵抛物线与x轴的两个交点坐标分别是(-1,0),(3,0),
∴-1×3=-3,
∴
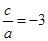 ,则a=-
,则a=-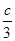 .
.∵抛物线与y轴的交点在(0,2)、(0,3)之间(包含端点),
∴2≤c≤3,
∴-1≤-
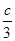 ≤-
≤-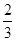 ,即-1≤a≤-
,即-1≤a≤-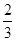 .
.故③正确;
④根据题意知,a=-
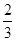 ,-
,-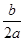 =1,
=1,∴b=-2a=
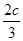 ,
,∴n=a+b+c=
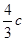
∵2≤c≤3,
∴
 ≤
≤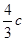 ≤4,即
≤4,即 ≤n≤4.
≤n≤4.故④错误.
综上所述,正确的说法有①③.
故选D.

练习册系列答案
相关题目
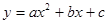 的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.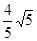 ,求点M的坐标.
,求点M的坐标.
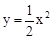 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交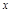 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.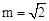 时,求S的值.
时,求S的值.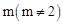 的函数解析式.
的函数解析式.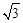 时,求
时,求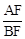 的值;
的值;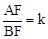 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.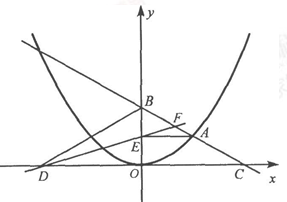
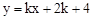 与抛物线
与抛物线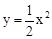 交于A、B两点,
交于A、B两点,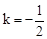 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
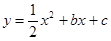 经过A(
经过A(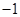 ,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.