Question

【题目】如图，E是正方形ABCD中CD边上一点，以点A为中心把△ADE顺时针旋转90°。

（1）在图中画出旋转后的图形；

（2）若旋转后E点的对应点记为M，点F在BC上，且∠EAF=45°，连接EF。

①求证：△AMF≌△AEF；

②若正方形的边长为6，AE＝，求EF的长．

Answer 1

【答案】（1）详见解析；（2）①详见解析；②5.

【解析】

试题（1）在CB的延长线上截取BM=DE，则△ABM满足条件；

（2）①由旋转性质得AM=AE，∠MAE=90°，则∠MAF=∠EAF=45°，根据SAS判断△AMF≌△AEF；

（3）由△AMF≌△AEF得EF=MF，再加上BM=DE，所以EF=BF+DE，由勾股定理计算出DE=3，则CE=3，设EF=x，则BF=x﹣3，CF=9﹣x，然后在Rt△CEF中利用勾股定理得到 (9﹣x)2+32=x2，解出x即可．

试题解析：（1）解：如图，△ABM为所作；

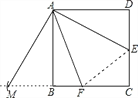
（2）①证明：∵ABCD 是正方形，∴∠BAD=90°，

∵△ADE绕点A顺时针旋转90°得到△ABM，

∴AM=AE，∠MAE=90°，

又∵∠EAF=45°，

∴∠MAF=45°，

∴∠MAF=∠EAF，

在△AMF和△AEF中，，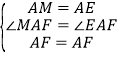

∴△AMF≌△AEF；

②：∵△AMF≌△AEF，

∴EF=MF，即MF=BF+MB，而BM=DE，

∴EF=BF+DE，

在Rt△ADE中

，DE=，

∴CE=6﹣3=3，设EF=x，则BF=x﹣3，

∴CF=6﹣(x﹣3)=9﹣x，在Rt△CEF中，

∵CF2+CE2=EF2，

∴(9﹣x)2+32=x2，

解得x=5，解EF=5．