题目内容
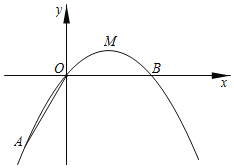
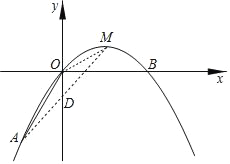
【题目】如图,在平面直角坐标系中,顶点为M的抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120°.
(1)求该抛物线的表达式;
(2)联结AM,求S△AOM;
(3)将抛物线C1向上平移得到抛物线C2,抛物线C2与x轴分别交于点E、F(点E在点F的左侧),如果△MBF与△AOM相似,求所有符合条件的抛物线C2的表达式.
【答案】(1)y=![]() ;(2)S△AOM=
;(2)S△AOM=![]() ;(3)y=
;(3)y=![]() ;y=
;y=![]() .
.
【解析】
(1)根据题意,可以写出点B和点A的坐标,从而可以得到该抛物线的表达式;
(2)根据(1)中的函数解析式,可以求得点M的坐标,从而可以求得直线AM的函数解析式,从而可以求得S△AOM;
(3)根据题意,利用分类讨论的方法和三角形相似的知识可以求得点F的坐标,从而可以求得抛物线C2的表达式.
(1)∵抛物线C1:y=ax2+bx(a<0)经过点A和x轴上的点B,AO=OB=2,∠AOB=120°,
∴点B(2,0),点A(﹣1,﹣![]() ),
),
∴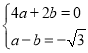 ,
,
得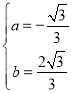 ,
,
∴该抛物线的解析式为y=![]() ;
;
(2)连接MO,AM,AM与y轴交于点D,
∵y=![]() =
=![]() ,
,
∴点M的坐标为(1,![]() ),
),
设过点A(﹣1,﹣![]() ),M(1,
),M(1,![]() )的直线解析式为y=mx+n,
)的直线解析式为y=mx+n,
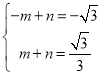 ,得
,得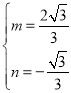 ,
,
∴直线AM的函数解析式为y=![]() x﹣
x﹣![]() ,
,
当x=0时,y=﹣![]() ,
,
∴点D的坐标为(0,﹣![]() ),
),
∴OD=![]() ,
,
∴S△AOM=S△AOD+S△MOD= ;
;
(3)当△AOM∽△FBM时,![]() ,
,
∵OA=2,点O(0,0),点M(1,![]() ),点B(2,0),
),点B(2,0),
∴OM=![]() ,BM=
,BM=![]() ,
,
∴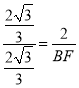 ,
,
解得,BF=2,
∴点F的坐标为(4,0),
设抛物线C2的函数解析式为:y=![]() +c,
+c,
∵点F(4,0)在抛物线C2上,
∴0=![]() +c,得c=
+c,得c=![]() ,
,
∴抛物线C2的函数解析式为:y=![]() +
+![]() ;
;
当△AOM∽△MBF时,
![]() ,
,
∵OA=2,点O(0,0),点M(1,![]() ),点B(2,0),
),点B(2,0),
∴OM=![]() ,BM=
,BM=![]() ,
,
∴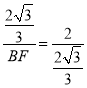 ,
,
解得,BF=![]() ,
,
∴点F的坐标为(![]() ,0),
,0),
设抛物线C2的函数解析式为:y=![]() +d,
+d,
∵点F(![]() ,0)在抛物线C2上,
,0)在抛物线C2上,
∴0=![]() ,得d=
,得d=![]() ,
,
∴抛物线C2的函数解析式为:y=![]() +
+![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】结论开放某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行调查.依据所有调查数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
类别 | 人数 | 占总人数的比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |

(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?