题目内容
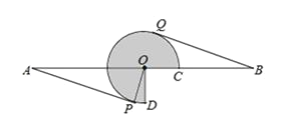
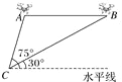
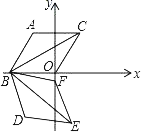
【题目】如图所示，菱形ABOC，其一边OB在x轴上，将菱形ABOC绕点B顺时针旋转75°至FBDE的位置，若BO＝2，∠A＝120°，则点E的坐标为（ ）
A. （
）B. （
）C. （
）D. （
）
【答案】A
【解析】
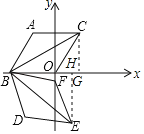
过C作CG⊥OB于G，过E作EH⊥OB于H，根据菱形的性质得到∠ABO＝60°，解直角三角形即可得到结论．
解：过C作CG⊥OB于G，过E作EH⊥OB于H，
在菱形ABOC中，∵∠A＝120°，AC∥BO，
∴∠ABO＝60°，
∴∠CBO＝30°，
∵BO＝CO＝2，∠COG＝60°，
在Rt△COG中，OG＝OCcos60°＝1，
∴BG＝1+2＝3，
在Rt△BCG中，BC＝
，
∵∠HBE＝75°﹣30°＝45°，
在Rt△BHE中，BH＝HE＝BEsin45°＝
，
∴OH＝
，
∴点E的坐标为（，
）．
故选：A．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
【题目】某校积极参与垃圾分类活动，以班级为单位收集可回收的垃圾，下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图（每组含前一个边界值，不含后一个边界值）.
某校七年级各班一周收集的可回收垃圾的质量频数表
组别（kg） | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
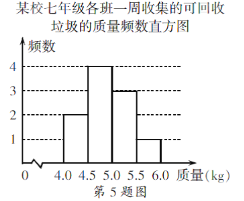
（1）求a的值；
（2）已知收集的可回收垃圾以0.8元/kg被回收，该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
