Question

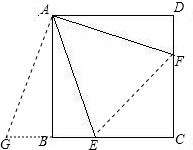
如图，正方形ABCD中，E、F分别在边BC、CD上，∠EAF=45°，BE=2，CF=3．求：正方形的边长．如图，正方形ABCD中，E、F分别在边BC、CD上，∠EAF=45°，BE=2，CF=3．求：正方形的边长．

Answer 1

延长CB至G，使BG=DF，连接AG、EF，
设正方形的边长为a，则DF=a-3，CE=a-2，
∵AB=AD，BG=DF，∠GBA=∠FDA=90°，
∴△ABG≌△ADF，（SAS）
∴∠GAB=∠FAD，AG=AF，
∵∠EAF=45°，∠BAD=90°，
∴∠GAE=45°，
∵AF=AG，∠EAF=∠EAG=45°，AE=AE，
∴△AEF≌△AEG，
∴EF=EG，
在Rt△CEF中，EF=

CF2+CE2

=

32+(a-2)2

，
在△AEG中，EG=EB+BG=a-3+2=a-1，
∴

32+(a-2)2

=a-1，
∴a=6，
∴正方形的边长为6．