题目内容
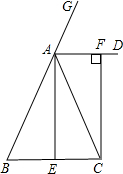
如图,将一三角板放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动, 直角的一边始终经过点B,另一边与射线DC相交于Q.
直角的一边始终经过点B,另一边与射线DC相交于Q.
探究:设A、P两点间的距离为x.
(1)当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系,并写出函数自变量x的取值范围;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置.并求出相应的x值,如果不可能,试说明理由.
 直角的一边始终经过点B,另一边与射线DC相交于Q.
直角的一边始终经过点B,另一边与射线DC相交于Q.探究:设A、P两点间的距离为x.
(1)当点Q在边CD上时,线段PQ与PB之间有怎样的数量关系?试证明你的猜想;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数关系,并写出函数自变量x的取值范围;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置.并求出相应的x值,如果不可能,试说明理由.
(1)PQ=PB,(1分)
过P点作MN∥BC分别交AB、DC于点M、N,
在正方形ABCD中,AC为对角线,
∴AM=PM,
又∵AB=MN,
∴MB=PN,
∵∠BPQ=90°,
∴∠BPM+∠NPQ=90°;
又∵∠MBP+∠BPM=90°,
∴∠MBP=∠NPQ,
在Rt△MBP≌Rt△NPQ中,
∵
∴Rt△MBP≌Rt△NPQ,(2分)
∴PB=PQ.
(2)∵S四边形PBCQ=S△PBC+S△PCQ,
∵AP=x,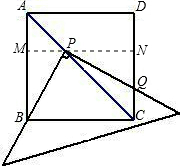
∴AM=
x,
∴CQ=CD-2NQ=1-
x,
又∵S△PBC=
BC•BM=
•1•(1-
x)=
-
x,
S△PCQ=
CQ•PN=
(1-
x)•(1-
x),
=
x2-
x+
,
∴S四边形PBCQ=
x2-
x+1.(0≤x≤
).(4分)
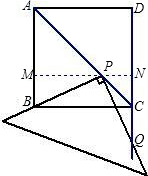
(3)△PCQ可能成为等腰三角形.
①当点P与点A重合时,点Q与点D重合,
PQ=QC,此时,x=0.(5分)
②当点Q在DC的延长线上,且CP=CQ时,(6分)
有:QN=AM=PM=
x,CP=
-x,CN=
CP=1-
x,CQ=QN-CN=
x-(1-
x)=
x-1,
∴当
-x=
x-1时,x=1.(7分).
过P点作MN∥BC分别交AB、DC于点M、N,
在正方形ABCD中,AC为对角线,
∴AM=PM,
又∵AB=MN,
∴MB=PN,
∵∠BPQ=90°,
∴∠BPM+∠NPQ=90°;
又∵∠MBP+∠BPM=90°,
∴∠MBP=∠NPQ,
在Rt△MBP≌Rt△NPQ中,
∵
|
∴Rt△MBP≌Rt△NPQ,(2分)
∴PB=PQ.
(2)∵S四边形PBCQ=S△PBC+S△PCQ,
∵AP=x,

∴AM=
| ||
| 2 |
∴CQ=CD-2NQ=1-
| 2 |
又∵S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
∴S四边形PBCQ=
| 1 |
| 2 |
| 2 |
| ||
| 2 |

(3)△PCQ可能成为等腰三角形.
①当点P与点A重合时,点Q与点D重合,
PQ=QC,此时,x=0.(5分)
②当点Q在DC的延长线上,且CP=CQ时,(6分)
有:QN=AM=PM=
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
∴当
| 2 |
| 2 |

练习册系列答案
相关题目