题目内容
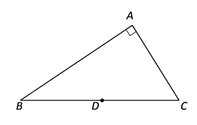
【题目】如图,在△ABC中,∠A=90°,∠B=36°,点D为斜边BC的中点,将线段DC绕着点D逆时针旋转任意角度得到线段DE(点E不与A、B、C重合),连接EA,EC,则∠AEC=___________°.
【答案】36或144
【解析】
根据旋转的性质及直角三角形的性质可知DC=DA=DE,点C,A,E三点共圆,从而利用同弧所对的圆周角相等,圆内接四边形对角互补求解.
解:∵在△ABC中,∠A=90°,∠B=36°,点D为斜边BC的中点
∴DA=DC
又∵线段DC绕着点D逆时针旋转任意角度得到线段DE
∴DC=DA=DE,
即点C,A,E三点在以D为圆心,DC为半径的圆上
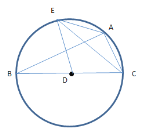
根据同弧所对的圆周角相等,此时∠AEC=∠ABC=36°;
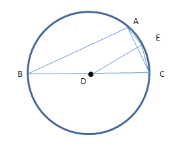
根据圆内接四边形对角互补,此时∠AEC+∠ABC=180°
∴∠AEC=180°-36°=144°,
故答案为:36或144.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目