题目内容
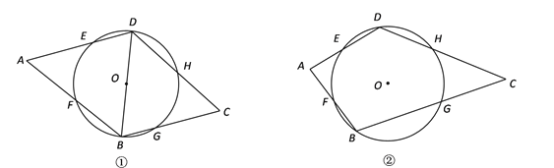
【题目】已知⊙O经过四边形ABCD的B、D两点,并与四条边分别交于点E、F、G、H,且![]() .
.
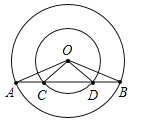
(1)如图①,连接BD,若BD是⊙O的直径,求证:∠A=∠C;
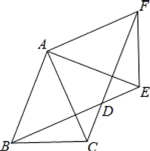
(2)如图②,若![]() 的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
的度数为θ,∠A=α,∠C=β,请直接写出θ、α和β之间的数量关系.
【答案】(1)证明见解析;(2)α+β+θ =180°
【解析】
(1)根据圆周角定理及同弧所对的圆周角相等,得到∠EDF=∠HDG,然后利用外角的性质等量代换求证;
(2)利用外角性质及圆内接四边形对角互补求解.
(1) 连接DF、DG
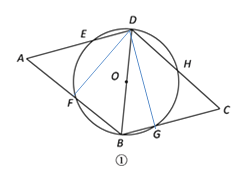
∵BD是⊙O的直径
∴∠DFB=∠DGB =90°,
∵![]()
∴∠EDF=∠HDG,
∵∠DFB=∠EDF+∠A
∠DGB=∠HDG+∠C,
∴∠A=∠C
(2)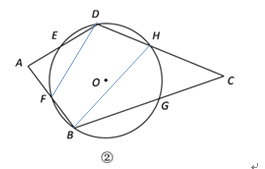
连接DF,BH
∵![]()
∴∠ADF=∠HBG=![]() θ
θ
又∵∠DFB=∠A+∠ADF,∠DHB=∠C+∠HBG
∴∠DFB+∠DHB=∠A+∠ADF+∠C+∠HBG
根据圆内接四边形对角互补,可得
∴α+β+θ =180°

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目