题目内容
【题目】如图①,菱形ABCD中,AB=5cm,动点P从点B出发,沿折线BC﹣CD﹣DA运动到点A停止,动点Q从点A出发,沿线段AB运动到点B停止,它们运动的速度相同,设点P出发xs时,△BPQ的面积为ycm2 , 已知y与x之间的函数关系如图②所示,其中OM,MN为线段,曲线NK为抛物线的一部分,请根据图中的信息,解答下列问题: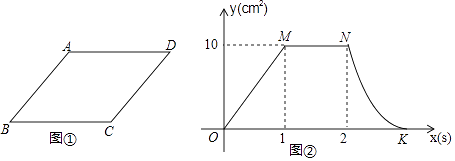
(1)当1<x<2时,△BPQ的面积(填“变”或“不变”);
(2)分别求出线段OM,曲线NK所对应的函数表达式;
(3)当x为何值时,△BPQ的面积是5cm2?
【答案】
(1)不变
(2)
解:设线段OM的函数表达式为y=kx,
把(1,10)代入得,k=10,
∴线段OM的函数表达式为y=10x;
设曲线NK所对应的函数表达式y=a(x﹣3)2,
把(2,10)代入得,10=a(2﹣3)2,
∴a=10,
∴曲线NK所对应的函数表达式y=10(x﹣3)2;
(3)
解:把y=5代入y=10x得,x= ![]() ,
,
把y=5代入y=10(x﹣3)2得,5=10(x﹣3)2,
∴x=3± ![]() ,
,
∵3+ ![]() >3,
>3,
∴x=3﹣ ![]() ,
,
∴当x= ![]() 或3﹣
或3﹣ ![]() 时,△BPQ的面积是5cm2.
时,△BPQ的面积是5cm2.
【解析】解:(1)由函数图象知,当1<x<2时,△BPQ的面积始终等于10,
∴当1<x<2时,△BPQ的面积不变;
所以答案是:不变;
【考点精析】利用函数的图象对题目进行判断即可得到答案,需要熟知函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.

【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.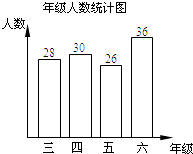
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
根据图表中提供的信息,回答下列问题:
(1)请将统计表补充完整
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
(2)测试学生中,成绩为80分的学生人数有 名;众数是 分;中位数是 分;
(3)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有 名.
【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形图中区域 | D | E | C |

如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?







