Question

【题目】已知：如图所示，在平面直角坐标系xoy中，四边形OABC是矩形，OA=4，OC=3，动点P从点C出发，沿射线CB方向以每秒2个单位长度的速度运动；同时，动点Q从点O出发，沿x轴正半轴方向以每秒1个单位长度的速度运动．设点P、点Q的运动时间为t（s）．

（1）当t=1s时，求经过点O，P，A三点的抛物线的解析式；
（2）当t=2s时，求tan∠QPA的值；
（3）当线段PQ与线段AB相交于点M，且BM=2AM时，求t（s）的值；
（4）连接CQ，当点P，Q在运动过程中，记△CQP与矩形OABC重叠部分的面积为S，求S与t的函数关系式．

Answer 1

【答案】
（1）

解：当t=1s时，则CP=2，

∵OC=3，四边形OABC是矩形，

∴P（2，3），且A（4，0），

∵抛物线过原点O，

∴可设抛物线解析式为y=ax2+bx，

∴ ，解得 ，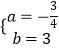

∴过O、P、A三点的抛物线的解析式为y=﹣ x2+3x；

（2）

解：当t=2s时，则CP=2×2=4=BC，即点P与点B重合，OQ=2，如图1，

∴AQ=OA﹣OQ=4﹣2=2，且AP=OC=3，

∴tan∠QPA= = ；

（3）

解：当线段PQ与线段AB相交于点M，则可知点Q在线段OA上，点P在线段CB的延长线上，如图2，

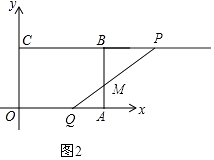
则CP=2t，OQ=t，

∴BP=PC﹣CB=2t﹣4，AQ=OA﹣OQ=4﹣t，

∵PC∥OA，

∴△PBM∽△QAM，

∴ = ，且BM=2AM，

∴ =2，解得t=3，

∴当线段PQ与线段AB相交于点M，且BM=2AM时，t为3s；

（4）

解：当0≤t≤2时，如图3，

由题意可知CP=2t，

∴S=S△PCQ= ×2t×3=3t；

当2＜t≤4时，设PQ交AB于点M，如图4，

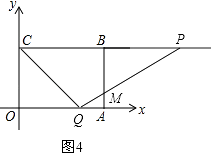
由题意可知PC=2t，OQ=t，则BP=2t﹣4，AQ=4﹣t，

同（3）可得 = = ，

∴BM= AM，

∴3﹣AM= AM，解得AM= ，

∴S=S四边形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ=3×4﹣ ×t×3﹣ ×（4﹣t）× =24﹣ ﹣3t；

当t＞4时，设CQ与AB交于点M，如图5，

由题意可知OQ=t，AQ=t﹣4，

∵AB∥OC，

∴ = ，即 = ，解得AM= ，

∴BM=3﹣ = ，

∴S=S△BCM= ×4× = ；

综上可知S= ．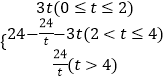

【解析】（1）可求得P点坐标，由O、P、A的坐标，利用待定系数法可求得抛物线解析式；（2）当t=2s时，可知P与点B重合，在Rt△ABQ中可求得tan∠QPA的值；（3）用t可表示出BP和AQ的长，由△PBM∽△QAM可得到关于t的方程，可求得t的值；（4）当点Q在线段OA上时，S=S△CPQ；当点Q在线段OA上，且点P在线段CB的延长线上时，由相似三角形的性质可用t表示出AM的长，由S=S四边形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ ， 可求得S与t的关系式；当点Q在OA的延长线上时，设CQ交AB于点M，利用△AQM∽△BCM可用t表示出AM，从而可表示出BM，S=S△CBM ， 可求得答案．
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．