题目内容
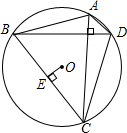
如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于( )

| A.20° | B.30° | C.40° | D.50° |

连接OD,
∵AO=OC=OD,DA=DC,
∴△ADO≌△CDO.
∴∠COD=∠AOD=
∠AOC=80°.
∴∠ODC=∠OCD=∠ODA=∠OAD=50°.
∴∠CDA=100°.
∵AD∥BC,
∴∠DCB=180°-∠CDA=180°-100°=80°.
∴∠BCO=∠BCD-∠OCD=80°-50°=30°.
故选B.

∵AO=OC=OD,DA=DC,
∴△ADO≌△CDO.
∴∠COD=∠AOD=
| 1 |
| 2 |
∴∠ODC=∠OCD=∠ODA=∠OAD=50°.
∴∠CDA=100°.
∵AD∥BC,
∴∠DCB=180°-∠CDA=180°-100°=80°.
∴∠BCO=∠BCD-∠OCD=80°-50°=30°.
故选B.


练习册系列答案
相关题目