题目内容
【题目】有一块等腰三角形白铁皮余料ABC,它的腰AB=10cm,底边BC=12cm.
(1)圆圆同学想从中裁出最大的圆,请帮他求出该圆的半径;
(2)方方同学想从中裁出最大的正方形,请帮他求出该正方形的边长.
【答案】(1)等腰三角形中裁出最大的圆的半径为3cm;(2)等腰三角形中裁出最大的正方形的边长为![]() cm.
cm.
【解析】
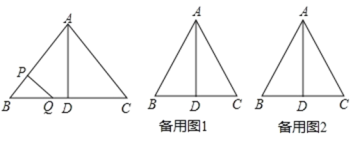
(1)如图1,⊙O为等腰△ABC的内切圆,作AD⊥BC于D,利用等腰三角形的性质得BD=CD=6,利用勾股定理得AD=8,设⊙O的半径为R,利用切线的性质和三角形面积公式得到![]() (AB+AC+BC)=
(AB+AC+BC)=![]() AD×BC,从而可求出半径r;
AD×BC,从而可求出半径r;
(2)如图2,正方形EFGH为等腰△ABC的最大内接正方形,作高AD交EH于M,设正方形的边长为xcm,证明△AEH∽△ABC,利用相似比得到![]() ,然后解方程即可.
,然后解方程即可.
解:(1)如图1,⊙O为等腰△ABC的内切圆,作AD⊥BC于D,
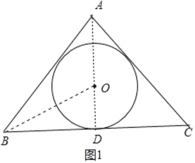
∵AB=AC,
∴BD=CD=6,
在Rt△ABD中,AD=![]() =8,
=8,
设⊙O的半径为R,
∵S△ABC=![]() ×r×(AB+AC+BC)=
×r×(AB+AC+BC)=![]() AD×BC,
AD×BC,
∴r=![]() =3,
=3,
答:等腰三角形中裁出最大的圆的半径为3cm;
(2)如图2,正方形EFGH为等腰△ABC的最大内接正方形,作高AD交EH于M,
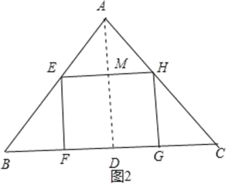
设正方形的边长为xcm,
由(1)得AD=8,则AM=8﹣x,
∵EH∥BC,
∴△AEH∽△ABC,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
答:等腰三角形中裁出最大的正方形的边长为![]() cm.
cm.

练习册系列答案
相关题目