Question

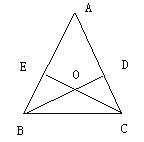
【题目】已知：如图，在△ABC中，AB=AC,BD、CE是高并交于点O.

求证：(1)BD=CE；（2）OB=OC.

Answer 1

【答案】（1）证明见解析；（2）证明见解析

【解析】试题分析：（1）利用面积可建立等式，根据AB=AC即可得出BD=CE；（2）欲证OB=OC，可证∠OBC=∠OCB，只要证明△BEC≌△CDB即可；由已知可得∠BEC=∠CDB=90°，BD=CE，BC是公共边，即可证得.

证明：（1）∵AB=AC,且BD、CE是高,

∴,

∴BD=CE.

（2）∵CE⊥AB，BD⊥AC，

∴△EBC和△DCB都是直角三角形，

在Rt△EBC与Rt△DCB中，

，

∴Rt△EBC≌Rt△DCB(HL)，

∴∠BCE=∠CBD，

∴OB=OC.